Implement with jsfiddle so people can see the specs and their code in the same window rather than a combo of editor/browser
SpecRunner.html in your web browserrecursion.jsspec/part1.js and
spec/part2.js as necessary
Recursion is when a function calls itself until it doesn’t. –not helpful person
Is it a true definition? Mostly. Recursion is when a function calls itself. A recursive function can call itself forever, but that’s generally not preferred. It’s often a good idea to include a condition in the function definition that allows it to stop calling itself. This condition is referred to as a base case. As a general rule, recursion shouldn’t be utilized without an accompanying base case unless an infinite operation is desired. This leaves us with two fundamental conditions every recursive function should include:
base case
recursive case
What does this all mean? Let’s consider a silly example:
function stepsToZero(n) {
if (n === 0) {
/* base case */
return "Reached zero";
} else {
/* recursive case */
console.log(n + " is not zero");
return stepsToZero(n - 1);
}
}
This function doesn’t do anything meaningful, but hopefully it
demonstrates the fundamental idea behind recursion. Simply put, recursion
provides us a looping or repeating mechanism. It repeats an operation
until a base condition is met. Let’s step through an
invocation of the above function to see how it evaluates.
stepsToZero(n) where n is the number
2
Invoke stepsToZero(n-1) where n-1 evaluates
to 1
Every recursive call adds a new invocation to the stack on top of the previous invocation
stepsToZero(n-1) where n-1 evaluates to
0
Return out of the initial invocation
Note that the value returned from the base case (step 9) gets returned to the previous invocation (step 4) on the stack. Step 4’s invocation takes that value and returns it to the invocation that preceded it (step 1). Once the initial invocation is reached, it returns the value to whatever invoked it. Through these steps, you can watch the call stack build up and once the base case is reached, the return value is passed back down as each invocation pops off the stack.
Due to the way the execution stack operates, it’s as if each function invocation pauses in time when a recursive call is made. The function that pauses before a recursive call will resume once the recursive call completes. If you’ve seen the movie Inception, this model may sound reminiscent to when the characters enter a person’s dreams and time slowed. The difference is time doesn’t actually slow with recursive invocations; rather, it’s a matter of order of operations. If a new invocation enters the execution stack, that invocation must complete before the previous can continue and complete.
Recursion can be elegant, but it can also be dangerous. In some cases, recursion feels like a more natural and readable solution; in others, it ends up being contrived. In most cases, recursion can be avoided entirely and sometimes should in order to minimize the possibility of exceeding the call stack and crashing your app. But keep in mind that code readability is important. If a recursive solution reads more naturally, then it may be the best solution for the given problem.
Recursion isn’t unique to any one programming language. As a software engineer, you will encounter recursion and it’s important to understand what’s happening and how to work with it. It’s also important to understand why someone might use it. Recursion is often used when the depth of a thing is unknown or every element of a thing needs to be touched. For example, you might use recursion if you want to find all DOM elements with a specific class name. You may not know how deep the DOM goes and need to touch every element so that none are missed. The same can be said for traversing any structure where all possible paths need to be considered and investigated.
Recursion is often used in divide and conquer algorithms where problems can be divided into similar subproblems and conquered individually. Consider traversing a tree structure. Each branch may have its own “children” branches. Every branch is essentially just another tree which means, as long as child trees are found, we can recurse on each child.
What’s the difference and connections between recursion, divide-and-conquer algorithm, dynamic programming, and greedy algorithm? If you haven’t made it clear. Doesn’t matter! I would give you a brief introduction to kick off this section.
What’s the difference and connections between recursion, divide-and-conquer algorithm, dynamic programming, and greedy algorithm? If you haven’t made it clear. Doesn’t matter! I would give you a brief introduction to kick off this section.
Recursion is a programming technique. It’s a way of thinking about solving problems. There’re two algorithmic ideas to solve specific problems: divide-and-conquer algorithm and dynamic programming. They’re largely based on recursive thinking (although the final version of dynamic programming is rarely recursive, the problem-solving idea is still inseparable from recursion). There’s also an algorithmic idea called greedy algorithm which can efficiently solve some more special problems. And it’s a subset of dynamic programming algorithms.
The divide-and-conquer algorithm will be explained in this section. Taking the most classic merge sort as an example, it continuously divides the unsorted array into smaller sub-problems. This is the origin of the word divide and conquer. Obviously, the sub-problems decomposed by the ranking problem are non-repeating. If some of the sub-problems after decomposition are duplicated (the nature of overlapping sub-problems), then the dynamic programming algorithm is used to solve them!
.
├── AUX_MATERIALS
│ ├── recursion-flow.PNG
│ ├── right.html
│ ├── sandbox
│ │ ├── LOs.js
│ │ ├── example2.js
│ │ ├── examples.js
│ │ ├── exponent.js
│ │ ├── factorial.js
│ │ ├── fibonacci.js
│ │ ├── flatten.js
│ │ ├── memoize.js
│ │ ├── recursiveCallStack.js
│ │ ├── recursiveIsEven.js
│ │ ├── recursiveRange.js
│ │ ├── right.html
│ │ ├── sum.js
│ │ └── tabulate.js
│ ├── solved.pdf
│ └── unzolved.pdf
├── README.html
├── README.md
├── blank
│ ├── README.md
│ ├── SpecRunner.html
│ ├── lib
│ │ ├── chai.js
│ │ ├── css
│ │ │ ├── mocha.css
│ │ │ └── right.html
│ │ ├── jquery.js
│ │ ├── mocha.js
│ │ ├── right.html
│ │ ├── sinon.js
│ │ └── testSupport.js
│ ├── right.html
│ ├── spec
│ │ ├── part1.js
│ │ ├── part2.js
│ │ └── right.html
│ ├── src
│ │ ├── recursion.js
│ │ └── right.html
│ └── testing
│ ├── directory1.html
│ ├── left1.html
│ ├── prism.css
│ ├── prism.js
│ ├── right.html
│ ├── right1.html
│ └── starter.html
├── dir.md
├── directory.html
├── images
│ ├── BubbleSort.gif
│ ├── InsertionSort.gif
│ ├── MergeSort.gif
│ ├── QuickSort.gif
│ ├── SLL-diagram.png
│ ├── SelectionSort.gif
│ ├── array-in-memory.png
│ ├── fib_memoized.png
│ ├── fib_tree.png
│ ├── fib_tree_duplicates.png
│ ├── github-repo-menu-bar-wiki.png
│ └── right.html
├── index.html
├── left.html
├── my-solutions
│ ├── README.md
│ ├── SpecRunner.html
│ ├── complete.html
│ ├── lib
│ │ ├── chai.js
│ │ ├── css
│ │ │ ├── mocha.css
│ │ │ └── right.html
│ │ ├── jquery.js
│ │ ├── mocha.js
│ │ ├── right.html
│ │ ├── sinon.js
│ │ └── testSupport.js
│ ├── prism.css
│ ├── prism.js
│ ├── right.html
│ ├── spec
│ │ ├── part1.js
│ │ ├── part2.js
│ │ └── right.html
│ ├── src
│ │ ├── recursion.js
│ │ └── right.html
│ └── style.css
├── part-2
│ ├── README.md
│ ├── SpecRunner.html
│ ├── lib
│ │ ├── jasmine-1.0.0
│ │ │ ├── MIT.LICENSE
│ │ │ ├── jasmine-html.js
│ │ │ ├── jasmine.css
│ │ │ ├── jasmine.js
│ │ │ └── right.html
│ │ ├── right.html
│ │ └── underscore.js
│ ├── right.html
│ ├── solutions
│ │ ├── binarySearchTree.js
│ │ ├── hashTable.js
│ │ ├── hashTableHelpers.js
│ │ ├── linkedList.js
│ │ ├── right.html
│ │ ├── set.js
│ │ └── tree.js
│ ├── spec
│ │ ├── binarySearchTreeSpec.js
│ │ ├── hashTableSpec.js
│ │ ├── linkedListSpec.js
│ │ ├── right.html
│ │ ├── setSpec.js
│ │ └── treeSpec.js
│ └── src
│ ├── binarySearchTree.js
│ ├── hashTable.js
│ ├── hashTableHelpers.js
│ ├── linkedList.js
│ ├── right.html
│ ├── set.js
│ └── tree.js
├── prism.css
├── prism.js
├── right.html
├── style.css
├── tabs
│ ├── right.html
│ ├── tabs.html
│ ├── tabs2.html
│ └── template-files
│ ├── LmfE5ZMlM8QjZWyylbaJdeYzodpJKK3mlCt6sCr3jaw.js
│ ├── about-us-page-template.jpg
│ ├── ad_status.js
│ ├── agency-template.jpg
│ ├── analytics.js
│ ├── application-template.jpg
│ ├── article-template.jpg
│ ├── base.js
│ ├── best-bootstrap-templates-492x492.jpg
│ ├── blog.jpg
│ ├── bootstrap-basic-template-492x492.jpg
│ ├── bootstrap-ecommerce-template-492x492.jpg
│ ├── bootstrap-grid.min.css
│ ├── bootstrap-landing-page-template-492x492.jpg
│ ├── bootstrap-layout-templates-492x492.jpg
│ ├── bootstrap-login-page-template-492x492.jpg
│ ├── bootstrap-one-page-template-492x492.jpg
│ ├── bootstrap-page-templates-492x492.jpg
│ ├── bootstrap-portfolio-template-600x600.jpg
│ ├── bootstrap-reboot.min.css
│ ├── bootstrap-responsive-website-templates-600x600.jpg
│ ├── bootstrap-sample-template-492x492.jpg
│ ├── bootstrap-single-page-template-492x492.jpg
│ ├── bootstrap-starter-template-492x492.jpg
│ ├── bootstrap-templates-examples-492x492.jpg
│ ├── bootstrap-theme-template-492x492.jpg
│ ├── bootstrap.min.css
│ ├── bootstrap.min.js
│ ├── business-template.jpg
│ ├── carousel-template.jpg
│ ├── cast_sender.js
│ ├── coming-soon-template.jpg
│ ├── contact-form-template-1.jpg
│ ├── corporate-template.jpg
│ ├── documentation-template.jpg
│ ├── download-bootstrap-template-492x492.jpg
│ ├── education-template.jpg
│ ├── embed.js
│ ├── error-template.jpg
│ ├── event-template.jpg
│ ├── f(1).txt
│ ├── f.txt
│ ├── faq-template.jpg
│ ├── fbevents.js
│ ├── fetch-polyfill.js
│ ├── footer-template.jpg
│ ├── form-templates.jpg
│ ├── free-html5-bootstrap-templates-600x600.jpg
│ ├── gallery-template.jpg
│ ├── google-maps-template.jpg
│ ├── grid-template.jpg
│ ├── gtm.js
│ ├── hGaQaBeUfGw.html
│ ├── header-template.jpg
│ ├── homepage-template.jpg
│ ├── hotel-template.jpg
│ ├── jarallax.min.js
│ ├── jquery.min.js
│ ├── jquery.touch-swipe.min.js
│ ├── landing-page-template.jpg
│ ├── list-template.jpg
│ ├── magazine-template.jpg
│ ├── map-template.jpg
│ ├── mbr-additional.css
│ ├── menu-template.jpg
│ ├── mobirise-icons.css
│ ├── multi-page-template.jpg
│ ├── navbar-template.jpg
│ ├── navigation-menu.jpg
│ ├── news-template.jpg
│ ├── one-page-1.jpg
│ ├── ootstrap-design-template-492x492.jpg
│ ├── parallax-scrolling-template.jpg
│ ├── parallax-template.jpg
│ ├── personal-website-template.jpg
│ ├── photo-gallery-template.jpg
│ ├── photography-template.jpg
│ ├── popper.min.js
│ ├── premium-bootstrap-templates-492x492.jpg
│ ├── profile-template.jpg
│ ├── real-estate-template.jpg
│ ├── registration-form-template.jpg
│ ├── remote.js
│ ├── restaurant-template.jpg
│ ├── right.html
│ ├── script.js
│ ├── script.min.js
│ ├── shopping-cart.jpg
│ ├── simple-bootstrap-template-492x492.jpg
│ ├── slider-template.jpg
│ ├── slider.jpg
│ ├── smooth-scroll.js
│ ├── social-network-template.jpg
│ ├── store-template.jpg
│ ├── style(1).css
│ ├── style.css
│ ├── tab-template.jpg
│ ├── table-template.jpg
│ ├── tether.min.css
│ ├── tether.min.js
│ ├── travel-template.jpg
│ ├── video-bg-template.jpg
│ ├── video-bg.jpg
│ ├── video-gallery-template.jpg
│ ├── video-template.jpg
│ ├── warren-wong-200912-2000x1304.jpg
│ ├── web-application-template.jpg
│ ├── wedding-template.jpg
│ ├── www-embed-player.js
│ └── www-player-webp.css
└── tree.md
22 directories, 227 files
Before introducing divide and conquer algorithm, we must first understand the concept of recursion.
The basic idea of recursion is that a function calls itself directly or indirectly, which transforms the solution of the original problem into many smaller sub-problems of the same nature. All we need is to focus on how to divide the original problem into qualified sub-problems, rather than study how this sub-problem is solved. The difference between recursion and enumeration is that enumeration divides the problem horizontally and then solves the sub-problems one by one, but recursion divides the problem vertically and then solves the sub-problems hierarchily.
The following illustrates my understanding of recursion. If you don’t want to read, please just remember how to answer these questions:
Two of the most important characteristics of recursive code: end conditions and self-invocation. Self-invocation is aimed at solving sub-problems, and the end condition defines the answer to the simplest sub-problem.
Actually think about it, what is the most successful application of recursion? I think it’s mathematical induction. Most of us learned mathematical induction in high school. The usage scenario is probably: we can’t figure out a summation formula, but we tried a few small numbers which seemed containing a kinda law, and then we compiled a formula. We ourselves think it shall be the correct answer. However, mathematics is very rigorous. Even if you’ve tried 10,000 cases which are correct, can you guarantee the 10001th correct? This requires mathematical induction to exert its power. Assuming that the formula we compiled is true at the kth number, furthermore if it is proved correct at the k + 1th, then the formula we have compiled is verified correct.
So what is the connection between mathematical induction and recursion? We just said that the recursive code must have an end condition. If not, it will fall into endless self-calling hell until the memory exhausted. The difficulty of mathematical proof is that you can try to have a finite number of cases, but it is difficult to extend your conclusion to infinity. Here you can see the connection-infinite.
The essence of recursive code is to call itself to solve smaller sub-problems until the end condition is reached. The reason why mathematical induction is useful is to continuously increase our guess by one, and expand the size of the conclusion, without end condition. So by extending the conclusion to infinity, the proof of the correctness of the guess is completed.
First to train the ability to think reversely. Recursive thinking is the thinking of normal people, always looking at the problems in front of them and thinking about solutions, and the solution is the future tense; Recursive thinking forces us to think reversely, see the end of the problem, and treat the problem-solving process as the past tense.
Second, practice analyzing the structure of the problem. When the problem can be broken down into sub problems of the same structure, you can acutely find this feature, and then solve it efficiently.
Third, go beyond the details and look at the problem as a whole. Let’s talk about merge and sort. In fact, you can divide the left and right areas without recursion, but the cost is that the code is extremely difficult to understand. Take a look at the code below (merge sorting will be described later. You can understand the meaning here, and appreciate the beauty of recursion).
void sort(Comparable[] a){
int N = a.length;
// So complicated! It shows disrespect for sorting. I refuse to study such code.
for (int sz = 1; sz < N; sz = sz + sz)
for (int lo = 0; lo < N - sz; lo += sz + sz)
merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, N - 1));
}
/* I prefer recursion, simple and beautiful */
void sort(Comparable[] a, int lo, int hi) {
if (lo >= hi) return;
int mid = lo + (hi - lo) / 2;
sort(a, lo, mid); // soft left part
sort(a, mid + 1, hi); // soft right part
merge(a, lo, mid, hi); // merge the two sides
}Looks simple and beautiful is one aspect, the key is very interpretable: sort the left half, sort the right half, and finally merge the two sides. The non-recursive version looks unintelligible, full of various incomprehensible boundary calculation details, is particularly prone to bugs and difficult to debug. Life is short, i prefer the recursive version.
Obviously, sometimes recursive processing is efficient, such as merge sort, sometimes inefficient, such as counting the hair of Monkey King, because the stack consumes extra space but simple inference does not consume space. Example below gives a linked list header and calculate its length:
My point of view: Understand what a function does and believe it can accomplish this task. Don’t try to jump into the details. Do not jump into this function to try to explore more details, otherwise you will fall into infinite details and cannot extricate yourself. The human brain carries tiny sized stack!
Let’s start with the simplest example: traversing a binary tree.
Above few lines of code are enough to wipe out any binary tree. What I
want to say is that for the recursive function
traverse (root) , we just need to believe: give it a root
node root , and it can traverse the whole tree. Since this
function is written for this specific purpose, so we just need to dump the
left and right nodes of this node to this function, because I believe it
can surely complete the task. What about traversing an N-fork tree? It’s
too simple, exactly the same as a binary tree!
As for pre-order, mid-order, post-order traversal, they are all obvious. For N-fork tree, there is obviously no in-order traversal.
The following explains a problem from LeetCode in detail: Given a binary tree and a target value, the values in every node is positive or negative, return the number of paths in the tree that are equal to the target value, let you write the pathSum function:
The problem may seem complicated, but the code is extremely concise, which is the charm of recursion. Let me briefly summarize the solution process of this problem:
First of all, it is clear that to solve the problem of recursive tree, you must traverse the entire tree. So the traversal framework of the binary tree (recursively calling the function itself on the left and right children) must appear in the main function pathSum. And then, what should they do for each node? They should see how many eligible paths they and their little children have under their feet. Well, this question is clear.
According to the techniques mentioned earlier, define what each recursive function should do based on the analysis just now:
PathSum function: Give it a node and a target value. It returns the total number of paths in the tree rooted at this node and the target value.
Count function: Give it a node and a target value. It returns a tree rooted at this node, and can make up the total number of paths starting with the node and the target value.
/* With above tips, comment out the code in detail */
int pathSum(TreeNode root, int sum) {
if (root == null) return 0;
int pathImLeading = count(root, sum); // Number of paths beginning with itself
int leftPathSum = pathSum(root.left, sum); // The total number of paths on the left (Believe he can figure it out)
int rightPathSum = pathSum(root.right, sum); // The total number of paths on the right (Believe he can figure it out)
return leftPathSum + rightPathSum + pathImLeading;
}
int count(TreeNode node, int sum) {
if (node == null) return 0;
// Can I stand on my own as a separate path?
int isMe = (node.val == sum) ? 1 : 0;
// Left brother, how many sum-node.val can you put together?
int leftBrother = count(node.left, sum - node.val);
// Right brother, how many sum-node.val can you put together?
int rightBrother = count(node.right, sum - node.val);
return isMe + leftBrother + rightBrother; // all count i can make up
}Again, understand what each function can do and trust that they can do it.
In summary, the binary tree traversal framework provided by the PathSum function calls the count function for each node during the traversal. Can you see the pre-order traversal (the order is the same for this question)? The count function is also a binary tree traversal, used to find the target value path starting with this node. Understand it deeply!
Merge and sort, typical divide-and-conquer algorithm; divide-and-conquer, typical recursive structure.
The divide-and-conquer algorithm can go in three steps: decomposition-> solve-> merge
To merge and sort, let’s call this function merge_sort .
According to what we said above, we must clarify the responsibility of the
function, that is, sort an incoming array. OK, can this
problem be solved? Of course! Sorting an array is just the same to sorting
the two halves of the array separately, and then merging the two halves.
Well, this algorithm is like this, there is no difficulty at all. Remember
what I said before, believe in the function’s ability, and pass it to him
half of the array, then the half of the array is already sorted. Have you
found it’s a binary tree traversal template? Why it is postorder
traversal? Because the routine of our divide-and-conquer algorithm is
decomposition-> solve (bottom)-> merge (backtracking)
Ah, first left and right decomposition, and then processing merge,
backtracking is popping stack, which is equivalent to post-order
traversal. As for the merge function, referring to the
merging of two ordered linked lists, they are exactly the same, and the
code is directly posted below.
Let’s refer to the Java code in book Algorithm 4 below, which
is pretty. This shows that not only algorithmic thinking is important, but
coding skills are also very important! Think more and imitate more.
public class Merge {
// Do not construct new arrays in the merge function, because the merge function will be called multiple times, affecting performance.Construct a large enough array directly at once, concise and efficient.
private static Comparable[] aux;
public static void sort(Comparable[] a) {
aux = new Comparable[a.length];
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (lo >= hi) return;
int mid = lo + (hi - lo) / 2;
sort(a, lo, mid);
sort(a, mid + 1, hi);
merge(a, lo, mid, hi);
}
private static void merge(Comparable[] a, int lo, int mid, int hi) {
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
for (int k = lo; k <= hi; k++) {
if (i > mid) { a[k] = aux[j++]; }
else if (j > hi) { a[k] = aux[i++]; }
else if (less(aux[j], aux[i])) { a[k] = aux[j++]; }
else { a[k] = aux[i++]; }
}
}
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
}LeetCode has a special exercise of the divide-and-conquer algorithm. Copy the link below to web browser and have a try:
https://leetcode.com/tag/divide-and-conquer/
Prompt: write a function that will reverse a string:
var reverse = function(string){
if(string.length < 2){
}
var first = string[0]
var last = string[string.length-1]; return last +reverse(string.slice(1,
string.length-1)) + first; }; reverse(‘abcdef’); //returns ‘fedcba’
//explain what a recursive function is
A function that calls itself is a recursive function.
If a function calls itself… then that function calls itself… then that function calls itself… well… then we have fallen into an infinite loop (a very unproductive place to be). To benefit from recursive calls, we need to be careful to include to give our interpreter a way to break out of the cycle of recursive function calls; we call this a base case.
The base case in the solution code above is as simple as testing that the length of the argument is less than 2… and if it is, returning the the value of that argument.
Notice how each time we recursively call the reverse function, we are passing it a shorter string argument… so each recursive call is getting us closer to hitting our base case.
//visualize the interpreter’s path through recursive function calls

Image for post
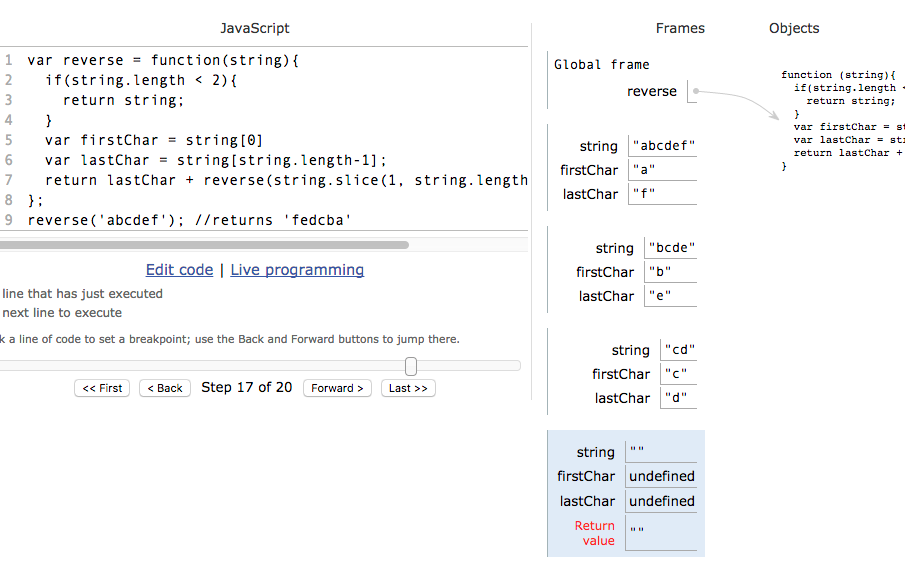
Image for post
Slow down and follow the interpreter through its execution of your algorithm (thanks to PythonTutor.com)
Python Tutor is an excellent resource for learning to visualize and trace variable values through the multiple execution contexts of a recursive function’s invocation.
Try it now with these simple steps:
//when can a recursive function help me?
So if I hope that at this point that you are thinking: there is a better way to reverse a function, or there is a simpler way to reverse a string…
First off… simpler is better. Writing good code isn’t about being clever or fancy; good code is about writing code that works, that makes sense to as many other minds as possible, that is time efficient, and that is memory efficient (in order of importance). As new programers, the first of these criteria is obvious, and the last two are given way too much weight. It’s the second of these criteria that needs to carry much more weight in our minds and deserves the most attention. Recursive functions can be a powerful tool in helping us write clear and simple solutions.
To be clear: recursion is not about being fancy or clever… it is an important skill to wrestle with early because there will be many scenarios when employing recursion will allow for a simpler and more reliable solution than would be possible without recursive functions.
//more useful example
Prompt: check to see if a binary-search-tree contains a value
var searchBST = function(tree, num){
if(tree.val === num){
} else if(num > tree.val){
} else{
}
}; var tree = {val: 9,
searchBST(tree, 4) // return falseWhen traversing trees and many other other non-primative data structures, recursion allows us to define a clear algorithm that elegantly handles uncertainty and complexity. Without recursion, it would be impossible to write a single function that could search a binary search tree of any size and state… yet by employing recursion, we can write a concise algorithm that will traverse any binary search tree and determine if it contains a value or not.
Take a moment to analyze how recursion is used in this example by tracing the interpreters path through this solution. Just as we did for the reverse function above, paste this binary search tree code snippet into the editor at http://pythontutor.com/javascript.html#mode=display
In this function definition, there are three base cases that will return a value instead of recursively calling the searchBST function… can you find them?
//now go practice using recursion
Big O Memoization And Tabulation - Recursion Videos - Curating Complexity: A Guide to Big-O Notation - Why Big-O? - Big-O Notation - Common Complexity Classes - The seven major classes - Memoization - Memoizing factorial - Memoizing the Fibonacci generator - The memoization formula - Tabulation - Tabulating the Fibonacci number - Aside: Refactoring for O(1) Space - Analysis of Linear Search - Analysis of Binary Search - Analysis of the Merge Sort - Analysis of Bubble Sort - LeetCode.com - Memoization Problems - Tabulation Problems
Sorting Algorithms - Bubble Sort - “But…then…why are we…” - The algorithm bubbles up - How does a pass of Bubble Sort work? - Ending the Bubble Sort - Pseudocode for Bubble Sort - Selection Sort - The algorithm: select the next smallest - The pseudocode - Insertion Sort - The algorithm: insert into the sorted region - The Steps - The pseudocode - Merge Sort - The algorithm: divide and conquer - Quick Sort - How does it work? - The algorithm: divide and conquer - The pseudocode - Binary Search - The Algorithm: “check the middle and half the search space” - The pseudocode - Bubble Sort Analysis - Time Complexity: O(n2) - Space Complexity: O(1) - When should you use Bubble Sort? - Selection Sort Analysis - Selection Sort JS Implementation - Time Complexity Analysis - Space Complexity Analysis: O(1) - When should we use Selection Sort? - Insertion Sort Analysis - Time and Space Complexity Analysis - When should you use Insertion Sort? - Merge Sort Analysis - Full code - Merging two sorted arrays - Divide and conquer, step-by-step - Time and Space Complexity Analysis - Quick Sort Analysis - Time and Space Complexity Analysis - Binary Search Analysis - Time and Space Complexity Analysis - Practice: Bubble Sort - Practice: Selection Sort - Practice: Insertion Sort - Practice: Merge Sort - Practice: Quick Sort - Practice: Binary Search
Lists, Stacks, and Queues - Linked Lists - What is a Linked List? - Types of Linked Lists - Linked List Methods - Time and Space Complexity Analysis - Time Complexity - Access and Search - Time Complexity - Insertion and Deletion - Space Complexity - Stacks and Queues - What is a Stack? - What is a Queue? - Stack and Queue Properties - Stack Methods - Queue Methods - Time and Space Complexity Analysis - When should we use Stacks and Queues? -
Graphs and Heaps - Introduction to Heaps - Binary Heap Implementation - Heap Sort - In-Place Heap Sort -
The objective of this lesson is get you comfortable with identifying the time and space complexity of code you see. Being able to diagnose time complexity for algorithms is an essential for interviewing software engineers.
At the end of this, you will be able to
At the end of this, you will be able to
The objective of this lesson is to give you a couple of ways to optimize a computation (algorithm) from a higher complexity class to a lower complexity class. Being able to optimize algorithms is an essential for interviewing software engineers.
At the end of this, you will be able to
At the end of this, you will be able to
A lot of algorithms that we use in the upcoming days will use recursion. The next two videos are just helpful reminders about recursion so that you can get that thought process back into your brain.
Colt Steele provides a very nice, non-mathy introduction to Big-O notation. Please watch this so you can get the easy introduction. Big-O is, by its very nature, math based. It’s good to get an understanding before jumping in to math expressions.
Complete Beginner’s Guide to Big O Notation by Colt Steele.
As software engineers, our goal is not just to solve problems. Rather, our goal is to solve problems efficiently and elegantly. Not all solutions are made equal! In this section we’ll explore how to analyze the efficiency of algorithms in terms of their speed (time complexity) and memory consumption (space complexity).
In this article, we’ll use the word efficiency to describe the amount of resources a program needs to execute. The two resources we are concerned with are time and space. Our goal is to minimize the amount of time and space that our programs use.
When you finish this article you will be able to:
Let’s begin by understanding what method we should not use when describing the efficiency of our algorithms. Most importantly, we’ll want to avoid using absolute units of time when describing speed. When the software engineer exclaims, “My function runs in 0.2 seconds, it’s so fast!!!”, the computer scientist is not impressed. Skeptical, the computer scientist asks the following questions:
The job of the software engineer is to focus on the software detail and not necessarily the hardware it will run on. Because we can’t answer points 1 and 2 with total certainty, we’ll want to avoid using concrete units like “milliseconds” or “seconds” when describing the efficiency of our algorithms. Instead, we’ll opt for a more abstract approach that focuses on point 3. This means that we should focus on how the performance of our algorithm is affected by increasing the size of the input. In other words, how does our performance scale?
The argument above focuses on time, but a similar argument could also be made for space. For example, we should not analyze our code in terms of the amount of absolute kilobytes of memory it uses, because this is dependent on the programming language.
In Computer Science, we use Big-O notation as a tool for describing the efficiency of algorithms with respect to the size of the input argument(s). We use mathematical functions in Big-O notation, so there are a few big picture ideas that we’ll want to keep in mind:
The first 3 points are conceptual, so they are easy to swallow. However, point 4 is typically the biggest source of confusion when learning the notation. Before we apply Big-O to our code, we’ll need to first understand the underlying math and simplification process.
We want our Big-O notation to describe the performance of our algorithm with respect to the input size and nothing else. Because of this, we should to simplify our Big-O functions using the following rules:
We’ll look at these rules in action, but first we’ll define a few things:
If a function consists of a product of many factors, we drop the factors that don’t depend on the size of the input, n. The factors that we drop are called constant factors because their size remains consistent as we increase the size of the input. The reasoning behind this simplification is that we make the input large enough, the non-constant factors will overshadow the constant ones. Below are some examples:
| Unsimplified | Big-O Simplified |
|---|---|
| T( 5 * n2 ) | O( n2 ) |
| T( 100000 * n ) | O( n ) |
| T( n / 12 ) | O( n ) |
| T( 42 * n * log(n) ) | O( n * log(n) ) |
| T( 12 ) | O( 1 ) |
Note that in the third example, we can simplify
T( n / 12 ) to O( n ) because we can rewrite a
division into an equivalent multiplication. In other words,
T( n / 12 ) = T( 1/12 * n ) = O( n ).
If the function consists of a sum of many terms, we only need to show the term that grows the fastest, relative to the size of the input. The reasoning behind this simplification is that if we make the input large enough, the fastest growing term will overshadow the other, smaller terms. To understand which term to keep, you’ll need to recall the relative size of our common math terms from the previous section. Below are some examples:
| Unsimplified | Big-O Simplified |
|---|---|
| T( n3 + n2 + n ) | O( n3 ) |
| T( log(n) + 2n ) | O( 2n ) |
| T( n + log(n) ) | O( n ) |
| T( n! + 10n ) | O( n! ) |
The product and sum rules are all we’ll need to Big-O simplify any math functions. We just apply the product rule to drop all constants, then apply the sum rule to select the single most dominant term.
| Unsimplified | Big-O Simplified |
|---|---|
| T( 5n2 + 99n ) | O( n2 ) |
| T( 2n + nlog(n) ) | O( nlog(n) ) |
| T( 2n + 5n1000) | O( 2n ) |
Aside: We’ll often omit the multiplication symbol in expressions as a form of shorthand. For example, we’ll write O( 5n2 ) in place of O( 5 * n2 ).
Analyzing the efficiency of our code seems like a daunting task because there are many different possibilities in how we may choose to implement something. Luckily, most code we write can be categorized into one of a handful of common complexity classes. In this reading, we’ll identify the common classes and explore some of the code characteristics that will lead to these classes.
When you finish this reading, you should be able to:
There are seven complexity classes that we will encounter most often. Below is a list of each complexity class as well as its Big-O notation. This list is ordered from smallest to largest. Bear in mind that a “more efficient” algorithm is one with a smaller complexity class, because it requires fewer resources.
| Big-O | Complexity Class Name |
|---|---|
| O(1) | constant |
| O(log(n)) | logarithmic |
| O(n) | linear |
| O(n * log(n)) | loglinear, linearithmic, quasilinear |
| O(nc) - O(n2), O(n3), etc. | polynomial |
| O(cn) - O(2n), O(3n), etc. | exponential |
| O(n!) | factorial |
There are more complexity classes that exist, but these are most common. Let’s take a closer look at each of these classes to gain some intuition on what behavior their functions define. We’ll explore famous algorithms that correspond to these classes further in the course.
For simplicity, we’ll provide small, generic code examples that illustrate the complexity, although they may not solve a practical problem.
Constant complexity means that the algorithm takes roughly the same number of steps for any size input. In a constant time algorithm, there is no relationship between the size of the input and the number of steps required. For example, this means performing the algorithm on a input of size 1 takes the same number of steps as performing it on an input of size 128.
The table below shows the growing behavior of a constant function. Notice that the behavior stays constant for all values of n.
| n | O(1) |
|---|---|
| 1 | ~1 |
| 2 | ~1 |
| 3 | ~1 |
| … | … |
| 128 | ~1 |
Below is are two examples of functions that have constant runtimes.
The runtime of the constant1 function does not depend on the
size of the input, because only two arithmetic operations (multiplication
and addition) are always performed. The runtime of the
constant2 function also does not depend on the size of the
input because one-hundred iterations are always performed, irrespective of
the input.
Typically, the hidden base of O(log(n)) is 2, meaning O(log2(n)). Logarithmic complexity algorithms will usual display a sense of continually “halving” the size of the input. Another tell of a logarithmic algorithm is that we don’t have to access every element of the input. O(log2(n)) means that every time we double the size of the input, we only require one additional step. Overall, this means that a large increase of input size will increase the number of steps required by a small amount.
The table below shows the growing behavior of a logarithmic runtime function. Notice that doubling the input size will only require only one additional “step”.
| n | O(log2(n)) |
|---|---|
| 2 | ~1 |
| 4 | ~2 |
| 8 | ~3 |
| 16 | ~4 |
| … | … |
| 128 | ~7 |
Below is an example of two functions with logarithmic runtimes.
The logarithmic1 function has O(log(n)) runtime because the
recursion will half the argument, n, each time. In other words, if we pass
8 as the original argument, then the recursive chain would be 8 -> 4
-> 2 -> 1. In a similar way, the logarithmic2 function
has O(log(n)) runtime because of the number of iterations in the while
loop. The while loop depends on the variable i, which will be
divided in half each iteration.
Linear complexity algorithms will access each item of the input “once” (in the Big-O sense). Algorithms that iterate through the input without nested loops or recurse by reducing the size of the input by “one” each time are typically linear.
The table below shows the growing behavior of a linear runtime function. Notice that a change in input size leads to similar change in the number of steps.
| n | O(n) |
|---|---|
| 1 | ~1 |
| 2 | ~2 |
| 3 | ~3 |
| 4 | ~4 |
| … | … |
| 128 | ~128 |
Below are examples of three functions that each have linear runtime.
The linear1 function has O(n) runtime because the for loop
will iterate n times. The linear2 function has O(n) runtime
because the for loop iterates through the array argument. The
linear3 function has O(n) runtime because each subsequent
call in the recursion will decrease the argument by one. In other words,
if we pass 8 as the original argument to linear3, the
recursive chain would be 8 -> 7 -> 6 -> 5 -> … -> 1.
This class is a combination of both linear and logarithmic behavior, so features from both classes are evident. Algorithms the exhibit this behavior use both recursion and iteration. Typically, this means that the recursive calls will halve the input each time (logarithmic), but iterations are also performed on the input (linear).
The table below shows the growing behavior of a loglinear runtime function.
| n | O(n * log2(n)) |
|---|---|
| 2 | ~2 |
| 4 | ~8 |
| 8 | ~24 |
| … | … |
| 128 | ~896 |
Below is an example of a function with a loglinear runtime.
The loglinear function has O(n * log(n)) runtime because the
for loop iterates linearly (n) through the input and the recursive chain
behaves logarithmically (log(n)).
Polynomial complexity refers to complexity of the form O(nc) where
n is the size of the input and c is some fixed
constant. For example, O(n3) is a larger/worse function than O(n2), but
they belong to the same complexity class. Nested loops are usually the
indicator of this complexity class.
Below are tables showing the growth for O(n2) and O(n3).
| n | O(n2) |
|---|---|
| 1 | ~1 |
| 2 | ~4 |
| 3 | ~9 |
| … | … |
| 128 | ~16,384 |
| n | O(n3) |
|---|---|
| 1 | ~1 |
| 2 | ~8 |
| 3 | ~27 |
| … | … |
| 128 | ~2,097,152 |
Below are examples of two functions with polynomial runtimes.
The quadratic function has O(n2) runtime because there are
nested loops. The outer loop iterates n times and the inner loop iterates
n times. This leads to n * n total number of iterations. In a similar way,
the cubic function has O(n3) runtime because it has triply
nested loops that lead to a total of n * n * n iterations.
Exponential complexity refers to Big-O functions of the form O(cn) where
n is the size of the input and c is some fixed
constant. For example, O(3n) is a larger/worse function than O(2n), but
they both belong to the exponential complexity class. A common indicator
of this complexity class is recursive code where there is a constant
number of recursive calls in each stack frame. The c will be
the number of recursive calls made in each stack frame. Algorithms with
this complexity are considered quite slow.
Below are tables showing the growth for O(2n) and O(3n). Notice how these grow large, quickly.
| n | O(2n) |
|---|---|
| 1 | ~2 |
| 2 | ~4 |
| 3 | ~8 |
| 4 | ~16 |
| … | … |
| 128 | ~3.4028 * 1038 |
| n | O(3n) |
|---|---|
| 1 | ~3 |
| 2 | ~9 |
| 3 | ~27 |
| 3 | ~81 |
| … | … |
| 128 | ~1.1790 * 1061 |
Below are examples of two functions with exponential runtimes.
The exponential2n function has O(2n) runtime because each
call will make two more recursive calls. The
exponential3n function has O(3n) runtime because each call
will make three more recursive calls.
Recall that n! = (n) * (n - 1) * (n - 2) * ... * 1. This
complexity is typically the largest/worst that we will end up
implementing. An indicator of this complexity class is recursive code that
has a variable number of recursive calls in each stack frame. Note that
factorial is worse than exponential because
factorial algorithms have a variable amount of recursive
calls in each stack frame, whereas exponential algorithms have a
constant amount of recursive calls in each frame.
Below is a table showing the growth for O(n!). Notice how this has a more aggressive growth than exponential behavior.
| n | O(n!) |
|---|---|
| 1 | ~1 |
| 2 | ~2 |
| 3 | ~6 |
| 4 | ~24 |
| … | … |
| 128 | ~3.8562 * 10215 |
Below is an example of a function with factorial runtime.
The factorial function has O(n!) runtime because the code is
recursive but the number of recursive calls made in a single
stack frame depends on the input. This contrasts with an
exponential function because exponential functions have a
fixed number of calls in each stack frame.
You may it difficult to identify the complexity class of a given code snippet, especially if the code falls into the loglinear, exponential, or factorial classes. In the upcoming videos, we’ll explain the analysis of these functions in greater detail. For now, you should focus on the relative order of these seven complexity classes!
In this reading, we listed the seven common complexity classes and saw some example code for each. In order of ascending growth, the seven classes are:
Recursion is the root of computation since it trades description for time.—Alan Perlis, Epigrams in Programming
In Arrays and Destructuring Arguments, we worked with the basic idea that putting an array together with a literal array expression was the reverse or opposite of taking it apart with a destructuring assignment.
We saw that the basic idea that putting an array together with a literal array expression was the reverse or opposite of taking it apart with a destructuring assignment.
Let’s be more specific. Some data structures, like lists, can obviously be seen as a collection of items. Some are empty, some have three items, some forty-two, some contain numbers, some contain strings, some a mixture of elements, there are all kinds of lists.
But we can also define a list by describing a rule for building lists. One of the simplest, and longest-standing in computer science, is to say that a list is:
Let’s convert our rules to array literals. The first rule is simple:
[] is a list. How about the second rule? We can express that
using a spread. Given an element e and a list
list , [e, ...list] is a list. We can test this
manually by building up a list:
Thanks to the parallel between array literals + spreads with destructuring + rests, we can also use the same rules to decompose lists:
For the purpose of this exploration, we will presume the following:1
Armed with our definition of an empty list and with what we’ve already
learned, we can build a great many functions that operate on arrays. We
know that we can get the length of an array using its
.length . But as an exercise, how would we write a
length function using just what we have already?
First, we pick what we call a terminal case. What is the length
of an empty array? 0 . So let’s start our function with the
observation that if an array is empty, the length is 0 :
We need something for when the array isn’t empty. If an array is not
empty, and we break it into two pieces, first and
rest , the length of our array is going to be
length(first) + length(rest) . Well, the length of
first is 1 , there’s just one element at the
front. But we don’t know the length of rest . If only there
was a function we could call… Like length !
Let’s try it!
Our length function is recursive, it calls itself.
This makes sense because our definition of a list is recursive, and if a
list is self-similar, it is natural to create an algorithm that is also
self-similar.
“Recursion” sometimes seems like an elaborate party trick. There’s even a joke about this:
When promising students are trying to choose between pure mathematics and applied engineering, they are given a two-part aptitude test. In the first part, they are led to a laboratory bench and told to follow the instructions printed on the card. They find a bunsen burner, a sparker, a tap, an empty beaker, a stand, and a card with the instructions “boil water.”
Of course, all the students know what to do: They fill the beaker with water, place the stand on the burner and the beaker on the stand, then they turn the burner on and use the sparker to ignite the flame. After a bit the water boils, and they turn off the burner and are lead to a second bench.
Once again, there is a card that reads, “boil water.” But this time, the beaker is on the stand over the burner, as left behind by the previous student. The engineers light the burner immediately. Whereas the mathematicians take the beaker off the stand and empty it, thus reducing the situation to a problem they have already solved.
There is more to recursive solutions that simply functions that invoke themselves. Recursive algorithms follow the “divide and conquer” strategy for solving a problem:
The big elements of divide and conquer are a method for decomposing a problem into smaller problems, a test for the smallest possible problem, and a means of putting the pieces back together. Our solutions are a little simpler in that we don’t really break a problem down into multiple pieces, we break a piece off the problem that may or may not be solvable, and solve that before sticking it onto a solution for the rest of the problem.
This simpler form of “divide and conquer” is called linear recursion. It’s very useful and simple to understand. Let’s take another example. Sometimes we want to flatten an array, that is, an array of arrays needs to be turned into one array of elements that aren’t arrays.2
We already know how to divide arrays into smaller pieces. How do we decide whether a smaller problem is solvable? We need a test for the terminal case. Happily, there is something along these lines provided for us:
The usual “terminal case” will be that flattening an empty array will produce an empty array. The next terminal case is that if an element isn’t an array, we don’t flatten it, and can put it together with the rest of our solution directly. Whereas if an element is an array, we’ll flatten it and put it together with the rest of our solution.
So our first cut at a flatten function will look like this:
Once again, the solution directly displays the important elements: Dividing a problem into subproblems, detecting terminal cases, solving the terminal cases, and composing a solution from the solved portions.
Another common problem is applying a function to every element of an array. JavaScript has a built-in function for this, but let’s write our own using linear recursion.
If we want to square each number in a list, we could write:
And if we wanted to “truthify” each element in a list, we could write:
This specific case of linear recursion is called “mapping,” and it is not necessary to constantly write out the same pattern again and again. Functions can take functions as arguments, so let’s “extract” the thing to do to each element and separate it from the business of taking an array apart, doing the thing, and putting the array back together.
Given the signature:
We can write it out using a ternary operator. Even in this small function, we can identify the terminal condition, the piece being broken off, and recomposing the solution.
With the exception of the length example at the beginning,
our examples so far all involve rebuilding a solution using spreads. But
they needn’t. A function to compute the sum of the squares of a list of
numbers might look like this:
There are two differences between sumSquares and our maps
above:
0 instead of an empty list, and;
sumSquares to the rest of the elements.
Let’s rewrite mapWith so that we can use it to sum squares.
And now we supply a function that does slightly more than our mapping functions:
Our foldWith function is a generalization of our
mapWith function. We can represent a map as a fold, we just
need to supply the array rebuilding code:
And if we like, we can write mapWith using
foldWith :
And to return to our first example, our version of length can
be written as a fold:
Linear recursion is a basic building block of algorithms. Its basic form parallels the way linear data structures like lists are constructed: This helps make it understandable. Its specialized cases of mapping and folding are especially useful and can be used to build other functions. And finally, while folding is a special case of linear recursion, mapping is a special case of folding.
undefined as a value, but we are not going to see that in
our examples. A more robust implementation would be
(array) => array.length === 0 , but we are doing
backflips to keep this within a very small and contrived playground.↩
flatten is a very simple
unfold, a
function that takes a seed value and turns it into an array. Unfolds can
be thought of a “path” through a data structure, and flattening a tree
is equivalent to a depth-first traverse.↩
Memoization is a design pattern used to reduce the overall number of calculations that can occur in algorithms that use recursive strategies to solve.
Recall that recursion solves a large problem by dividing it into smaller sub-problems that are more manageable. Memoization will store the results of the sub-problems in some other data structure, meaning that you avoid duplicate calculations and only “solve” each subproblem once. There are two features that comprise memoization:
This is a trade-off between the time it takes to run an algorithm (without memoization) and the memory used to run the algorithm (with memoization). Usually memoization is a good trade-off when dealing with large data or calculations.
You cannot always apply this technique to recursive problems. The problem must have an “overlapping subproblem structure” for memoization to be effective.
Here’s an example of a problem that has such a structure:
Using pennies, nickels, dimes, and quarters, what is the smallest combination of coins that total 27 cents?
You’ll explore this exact problem in depth later on. For now, here is some food for thought. Along the way to calculating the smallest coin combination of 27 cents, you should also calculate the smallest coin combination of say, 25 cents as a component of that problem. This is the essence of an overlapping subproblem structure.
Here’s an example of a function that computes the factorial of the number passed into it.
From this plain factorial above, it is clear that every time
you call factorial(6) you should get the same result of
720 each time. The code is somewhat inefficient because you
must go down the full recursive stack for each top level call to
factorial(6). It would be great if you could store the result
of factorial(6) the first time you calculate it, then on
subsequent calls to factorial(6) you simply fetch the stored
result in constant time. You can accomplish exactly this by memoizing with
an object!
The memo object above will map an argument of
factorial to its return value. That is, the keys will be
arguments and their values will be the corresponding results returned. By
using the memo, you are able to avoid duplicate recursive calls!
Here’s some food for thought: By the time your first call to
factorial(6) returns, you will not have just the argument
6 stored in the memo. Rather, you will have
all arguments 2 to 6 stored in the memo.
Hopefully you sense the efficiency you can get by memoizing your functions, but maybe you are not convinced by the last example for two reasons:
Both of those points are true, so take a look at a more advanced example that benefits from memoization.
Here’s a naive implementation of a function that calculates the Fibonacci number for a given input.
Before you optimize this, ask yourself what complexity class it falls into in the first place.
The time complexity of this function is not super intuitive to describe because the code branches twice recursively. Fret not! You’ll find it useful to visualize the calls needed to do this with a tree. When reasoning about the time complexity for recursive functions, draw a tree that helps you see the calls. Every node of the tree represents a call of the recursion:

fib_tree
In general, the height of this tree will be n. You derive
this by following the path going straight down the left side of the tree.
You can also see that each internal node leads to two more nodes. Overall,
this means that the tree will have roughly 2n nodes which is the same as
saying that the fib function has an exponential time
complexity of 2n. That is very slow! See for yourself, try running
fib(50) - you’ll be waiting for quite a while (it took 3
minutes on the author’s machine).
Okay. So the fib function is slow. Is there anyway to speed
it up? Take a look at the tree above. Can you find any repetitive regions
of the tree?

fib_tree_duplicates
As the n grows bigger, the number of duplicate sub-trees
grows exponentially. Luckily you can fix this using memoization by using a
similar object strategy as before. You can use some JavaScript default
arguments to clean things up:
The code above can calculate the 50th Fibonacci number almost instantly!
Thanks to the memo object, you only need to explore a subtree
fully once. Visually, the fastFib recursion has this
structure:

fib_memoized
You can see the marked nodes (function calls) that access the memo in
green. It’s easy to see that this version of the Fibonacci generator will
do far less computations as n grows larger! In fact, this
memoization has brought the time complexity down to linear
O(n) time because the tree only branches on the left side.
This is an enormous gain if you recall the complexity class hierarchy.
Now that you understand memoization, when should you apply it? Memoization is useful when attacking recursive problems that have many overlapping sub-problems. You’ll find it most useful to draw out the visual tree first. If you notice duplicate sub-trees, time to memoize. Here are the hard and fast rules you can use to memoize a slow function:
You learned a secret to possibly changing an algorithm of one complexity class to a lower complexity class by using memory to store intermediate results. This is a powerful technique to use to make sure your programs that must do recursive calculations can benefit from running much faster.
Now that you are familiar with memoization, you can explore a related method of algorithmic optimization: Tabulation. There are two main features that comprise the Tabulation strategy:
Many problems that can be solved with memoization can also be solved with tabulation as long as you convert the recursion to iteration. The first example is the canonical example of recursion, calculating the Fibonacci number for an input. However, in the example, you’ll see the iteration version of it for a fresh start!
Tabulation is all about creating a table (array) and filling it out with elements. In general, you will complete the table by filling entries from “left to right”. This means that the first entry of the table (first element of the array) will correspond to the smallest subproblem. Naturally, the final entry of the table (last element of the array) will correspond to the largest problem, which is also the final answer.
Here’s a way to use tabulation to store the intermediary calculations so that later calculations can refer back to the table.
When you initialized the table and seeded the first two values, it looked like this:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
table[i] |
0 |
1 |
After the loop finishes, the final table will be:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
table[i] |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
Similar to the previous memo, by the time the function
completes, the table will contain the final solution as well
as all sub-solutions calculated along the way.
To compute the complexity class of this tabulatedFib is very
straightforward since the code is iterative. The dominant operation in the
function is the loop used to fill out the entire table. The length of the
table is roughly n elements long, so the algorithm will have
an O(n) runtime. The space taken by our algorithm is also
O(n) due to the size of the table. Overall, this should be a
satisfying solution for the efficiency of the algorithm.
You may notice that you can cut down on the space used by the function. At any point of the loop, the calculation really only need the previous two subproblems’ results. There is little utility to storing the full array. This refactor is easy to do by using two variables:
Bam! You now have O(n) runtime and O(1) space. This is the most optimal algorithm for calculating a Fibonacci number. Note that this strategy is a pared down form of tabulation, since it uses only the last two values.
Here are the general guidelines for implementing the tabulation strategy. This is just a general recipe, so adjust for taste depending on your problem:
You learned another way of possibly changing an algorithm of one complexity class to a lower complexity class by using memory to store intermediate results. This is a powerful technique to use to make sure your programs that must do iterative calculations can benefit from running much faster.
Consider the following search algorithm known as linear search.
Most Big-O analysis is done on the “worst-case scenario” and provides an upper bound. In the worst case analysis, you calculate the upper bound on running time of an algorithm. You must know the case that causes the maximum number of operations to be executed.
For linear search, the worst case happens when the element to be
searched (term in the above code) is not present in the
array. When term is not present, the
search function compares it with all the elements of
array one by one. Therefore, the worst-case time complexity
of linear search would be O(n).
Consider the following search algorithm known as the binary search. This kind of search only works if the array is already sorted.
For the binary search, you cut the search space in half every time. This means that it reduces the number of searches you must do by half, every time. That means the number of steps it takes to get to the desired item (if it exists in the array), in the worst case takes the same amount of steps for every number within a range defined by the powers of 2.
So, for any number of items in the sorted array between 2n-1 and 2n, it takes n number of steps. That means if you have k items in the array, then it will take log2k.
Binary searches are O(log2n).
Consider the following divide-and-conquer sort method known as the merge sort.
For the merge sort, you cut the sort space in half every time. In each of those halves, you have to loop through the number of items in the array. That means that, for the worst case, you get that same log2n but it must be multiplied by the number of elements in the array, n.
Merge sorts are O(n*log2n).
Consider the following sort algorithm known as the bubble sort.
For the bubble sort, the worst case is the same as the best case because it always makes nested loops. So, the outer loop loops the number of times of the items in the array. For each one of those loops, the inner loop loops again a number of times for the items in the array. So, if there are n values in the array, then a loop inside a loop is n * n. So, this is O(n2). That’s polynomial, which ain’t that good.
use the LeetCode platform to check your work rather than relying on local mocha tests. If you don’t already have an account at LeetCode.com, please click https://leetcode.com/accounts/signup/ to sign up for a free account.
After you sign up for the account, please verify the account with the email address that you used so that you can actually run your solution on LeetCode.com.
In the projects, you will see files that are named “leet_code_«number».js”. When you open those, you will see a link in the file that you can use to go directly to the corresponding problem on LeetCode.com.
Use the local JavaScript file in Visual Studio Code to collaborate on the solution. Then, you can run the proposed solution in the LeetCode.com code runner to validate its correctness.
This project contains two test-driven problems and one problem on LeetCode.com.
cd into the project foldernpm install to install dependencies in the project root
directory
npx test to run the specs/test/test.js. Your job is
to write code in the /lib files to pass all specs.
problems.js, you will write code to make the
lucasNumberMemo and minChange functions
pass.
leet_code_518.js, you will use that file as a
scratch pad to work on the LeetCode.com problem at
https://leetcode.com/problems/coin-change-2/.
This project contains two test-driven problems and one problem on LeetCode.com.
cd into the project foldernpm install to install dependencies in the project root
directory
npx test to run the specs/test/test.js. Your job is
to write code in the /lib files to pass all specs.
problems.js, you will write code to make the
stepper, maxNonAdjacentSum, and
minChange functions pass.
leet_code_64.js, you will use that file as a scratch
pad to work on the LeetCode.com problem at
https://leetcode.com/problems/minimum-path-sum/.
leet_code_70.js, you will use that file as a scratch
pad to work on the LeetCode.com problem at
https://leetcode.com/problems/climbing-stairs/.
The objective of this lesson is for you to get experience implementing common sorting algorithms that will come up during a lot of interviews. It is also important for you to understand how different sorting algorithms behave when given output.
At the end of this, you will be able to
bubble sort on an array of numbers.
selection sort on an array of numbers.
insertion sort on an array of numbers.
merge sort on an array of numbers.
quick sort on an array of numbers.
At the end of this, you will be able to
bubble sort on an array of numbers.
selection sort on an array of numbers.
insertion sort on an array of numbers.
merge sort on an array of numbers.
quick sort on an array of numbers.
Bubble Sort is generally the first major sorting algorithm to come up in most introductory programming courses. Learning about this algorithm is useful educationally, as it provides a good introduction to the challenges you face when tasked with converting unsorted data into sorted data, such as conducting logical comparisons, making swaps while iterating, and making optimizations. It’s also quite simple to implement, and can be done quickly.
Bubble Sort is almost never a good choice in production. simply because:
It is quite useful as an educational base for you, and as a conversational base for you while interviewing, because you can discuss how other more elegant and efficient algorithms improve upon it. Taking naive code and improving upon it by weighing the technical tradeoffs of your other options is 100% the name of the game when trying to level yourself up from a junior engineer to a senior engineer.
As you progress through the algorithms and data structures of this course, you’ll eventually notice that there are some recurring funny terms. “Bubbling up” is one of those terms.
When someone writes that an item in a collection “bubbles up,” you should infer that:
When invoking Bubble Sort to sort an array of integers in ascending order, the largest integers will “bubble up” to the “top” (the end) of the array, one at a time.
The largest values are captured, put into motion in the direction defined by the desired sort (ascending right now), and traverse the array until they arrive at their end destination. See if you can observe this behavior in the following animation (courtesy http://visualgo.net):

bubble sort
As the algorithm iterates through the array, it compares each element to the element’s right neighbor. If the current element is larger than its neighbor, the algorithm swaps them. This continues until all elements in the array are sorted.
Bubble sort works by performing multiple passes to move elements closer to their final positions. A single pass will iterate through the entire array once.
A pass works by scanning the array from left to right, two elements at a time, and checking if they are ordered correctly. To be ordered correctly the first element must be less than or equal to the second. If the two elements are not ordered properly, then we swap them to correct their order. Afterwards, it scans the next two numbers and continue repeat this process until we have gone through the entire array.
See one pass of bubble sort on the array [2, 8, 5, 2, 6]. On
each step the elements currently being scanned are in
bold.
Because at least one swap occurred, the algorithm knows that it wasn’t sorted. It needs to make another pass. It starts over again at the first entry and goes to the next-to-last entry doing the comparisons, again. It only needs to go to the next-to-last entry because the previous “bubbling” put the largest entry in the last position.
Because at least one swap occurred, the algorithm knows that it wasn’t sorted. Now, it can bubble from the first position to the last-2 position because the last two values are sorted.
No swap occurred, so the Bubble Sort stops.
During Bubble Sort, you can tell if the array is in sorted order by checking if a swap was made during the previous pass performed. If a swap was not performed during the previous pass, then the array must be totally sorted and the algorithm can stop.
You’re probably wondering why that makes sense. Recall that a pass of Bubble Sort checks if any adjacent elements are out of order and swaps them if they are. If we don’t make any swaps during a pass, then everything must be already in order, so our job is done. Let that marinate for a bit.
Selection Sort is very similar to Bubble Sort. The major difference between the two is that Bubble Sort bubbles the largest elements up to the end of the array, while Selection Sort selects the smallest elements of the array and directly places them at the beginning of the array in sorted position. Selection sort will utilize swapping just as bubble sort did. Let’s carefully break this sorting algorithm down.
Selection sort works by maintaining a sorted region on the left side of the input array; this sorted region will grow by one element with every “pass” of the algorithm. A single “pass” of selection sort will select the next smallest element of unsorted region of the array and move it to the sorted region. Because a single pass of selection sort will move an element of the unsorted region into the sorted region, this means a single pass will shrink the unsorted region by 1 element whilst increasing the sorted region by 1 element. Selection sort is complete when the sorted region spans the entire array and the unsorted region is empty!

selection sort
The algorithm can be summarized as the following:
In pseudocode, the Selection Sort can be written as this.
With Bubble Sort and Selection Sort now in your tool box, you’re starting to get some experience points under your belt! Time to learn one more “naive” sorting algorithm before you get to the efficient sorting algorithms.
Insertion Sort is similar to Selection Sort in that it gradually builds up a larger and larger sorted region at the left-most end of the array.
However, Insertion Sort differs from Selection Sort because this algorithm does not focus on searching for the right element to place (the next smallest in our Selection Sort) on each pass through the array. Instead, it focuses on sorting each element in the order they appear from left to right, regardless of their value, and inserting them in the most appropriate position in the sorted region.
See if you can observe the behavior described above in the following animation:

insertion sort
Insertion Sort grows a sorted array on the left side of the input array by:
These steps are easy to confuse with selection sort, so you’ll want to watch the video lecture and drawing that accompanies this reading as always!
You’ve explored a few sorting algorithms already, all of them being quite slow with a runtime of O(n2). It’s time to level up and learn your first time-efficient sorting algorithm! You’ll explore merge sort in detail soon, but first, you should jot down some key ideas for now. The following points are not steps to an algorithm yet; rather, they are ideas that will motivate how you can derive this algorithm.
You’re going to need a helper function that solves the first major point
from above. How might you merge two sorted arrays? In other words you want
a merge function that will behave like so:
Once you have that, you get to the “divide and conquer” bit.
The algorithm for merge sort is actually really simple.
The process is visualized below. When elements are moved to the bottom of
the picture, they are going through the merge step:

merge sort
The pseudocode for the algorithm is as follows.
Quick Sort has a similar “divide and conquer” strategy to Merge Sort. Here are a few key ideas that will motivate the design:
Regarding that first point, for example given
[7, 3, 8, 9, 2] and a target of 5, we know
[3, 2] are numbers less than 5 and
[7, 8, 9] are numbers greater than 5.
In general, the strategy is to divide the input array into two subarrays: one with the smaller elements, and one with the larger elements. Then, it recursively operates on the two new subarrays. It continues this process until of dividing into smaller arrays until it reaches subarrays of length 1 or smaller. As you have seen with Merge Sort, arrays of such length are automatically sorted.
The steps, when discussed on a high level, are simple:
Before we move forward, see if you can observe the behavior described above in the following animation:

quick sort
Formally, we want to partition elements of an array relative to a pivot value. That is, we want elements less than the pivot to be separated from elements that are greater than or equal to the pivot. Our goal is to create a function with this behavior:
Seems simple enough! Let’s implement it in JavaScript:
You don’t have to use an explicit partition helper function
in your Quick Sort implementation; however, we will borrow heavily from
this pattern. As you design algorithms, it helps to think about key
patterns in isolation, although your solution may not feature that exact
helper. Some would say we like to divide and conquer.
It is so small, this algorithm. It’s amazing that it performs so well with so little code!
We’ve explored many ways to sort arrays so far, but why did we go through
all of that trouble? By sorting elements of an array, we are organizing
the data in a way that gives us a quick way to look up elements later on.
For simplicity, we have been using arrays of numbers up until this point.
However, these sorting concepts can be generalized to other data types.
For example, it would be easy to modify our comparison-based sorting
algorithms to sort strings: instead of leveraging facts like
0 < 1, we can say 'A' < 'B'.
Think of a dictionary. A dictionary contains alphabetically sorted words and their definitions. A dictionary is pretty much only useful if it is ordered in this way. Let’s say you wanted to look up the definition of “stupendous.” What steps might you take?
You are essentially using the binarySearch algorithm in the
real world.
Formally, our binarySearch will seek to solve the following
problem:
Programmatically, we want to satisfy the following behavior:
Before we move on, really internalize the fact that
binarySearch will only work on
sorted arrays! Obviously we can search any array, sorted
or unsorted, in O(n) time. But now our goal is be able to
search the array with a sub-linear time complexity (less than
O(n)).
Bubble Sort manipulates the array by swapping the position of two elements. To implement Bubble Sort in JS, you’ll need to perform this operation. It helps to have a function to do that. A key detail in this function is that you need an extra variable to store one of the elements since you will be overwriting them in the array:
Note that the swap function does not create or return a new array. It mutates the original array:
Take a look at the snippet below and try to understand how it corresponds to the conceptual understanding of the algorithm. Scroll down to the commented version when you get stuck.
Picture the worst case scenario where the input array is completely unsorted. Say it’s sorted in fully decreasing order, but the goal is to sort it in increasing order:
for loop along contributes O(n) in
isolation
n elements into their final resting positions.
It’s worth mentioning that the best case scenario is when the input array
is already fully sorted. This will cause our for loop to conduct a single
pass without performing any swap, so the while loop will not
trigger further iterations. This means best case time complexity is
O(n) for bubble sort. This best case linear time is probably the
only advantage of bubble sort. Programmers are usually interested only in
the worst-case analysis and ignore best-case analysis.
Bubble Sort is a constant space, O(1), algorithm. The amount of memory consumed by the algorithm does not increase relative to the size of the input array. It uses the same amount of memory and create the same amount of variables regardless of the size of the input, making this algorithm quite space efficient. The space efficiency mostly comes from the fact that it mutates the input array in-place. This is known as a destructive sort because it “destroys” the positions of the values in the array.
Nearly never, but it may be a good choice in the following list of special cases:
Since a component of Selection Sort requires us to locate the smallest value in the array, let’s focus on that pattern in isolation:
Pretty basic code right? We won’t use this explicit helper function to solve selection sort, however we will borrow from this pattern soon.
We’ll also utilize the classic swap pattern that we introduced in the bubble sort. To refresh:
Now for the punchline! Take a look at the snippet below and try to understand how it corresponds to our conceptual understanding of the selection sort algorithm. Scroll down to the commented version when you get stuck.
Selection Sort runtime is O(n2) because:
n is the length of the input arrayn = 10.
j will have 9 iterationsj will have 8 iterations
j will have 7 iterationsj will have 1 iterationYou’ll notice that during this analysis we said something silly like O(n / 2). In some analyses such as this one, we’ll prefer to drop the constants only at the end of the sketch so you understand the logical steps we took to derive a complicated time complexity.
The amount of memory consumed by the algorithm does not increase relative to the size of the input array. We use the same amount of memory and create the same amount of variables regardless of the size of our input. A quick indicator of this is the fact that we don’t create any arrays.
There is really only one use case where Selection Sort becomes superior to Bubble Sort. Both algorithms are quadratic in time and constant in space, but the point at which they differ is in the number of swaps they make.
Bubble Sort, in the worst case, invokes a swap on every single comparison. Selection Sort only swaps once our inner loop has completely finished traversing the array. Therefore, Selection Sort is optimized to make the least possible number of swaps.
Selection Sort becomes advantageous when making a swap is the most expensive operation in your system. You will likely rarely encounter this scenario, but in a situation where you’ve built (or have inherited) a system with suboptimal write speed ability, for instance, maybe you’re sorting data in a specialized database tuned strictly for fast read speeds at the expense of slow write speeds, using Selection Sort would save you a ton of expensive operations that could potential crash your system under peak load.
Though in industry this situation is very rare, the insights above make for a fantastic conversational piece when weighing technical tradeoffs while strategizing solutions in an interview setting. This commentary may help deliver the impression that you are well-versed in system design and technical analysis, a key indicator that someone is prepared for a senior level position.
Take a look at the snippet below and try to understand how it corresponds to our conceptual understanding of the Insertion Sort algorithm. Scroll down to the commented version when you get stuck:
There are a few key pieces to point out in the above solution before moving forward:
for loop starts at the 1st index, not the 0th
index, and moves to the right.
for loop starts immediately to the left of the
current element, and moves to the left.
for loop is complicated, and
behaves similarly to a while loop!
j = 0,
only while the currElement is less than
arr[j].
currElement, and then we exit the inner loop!
[1, 2, 4, 3], and currElement is
3, after comparing 4 and 3, but
before inserting 3 between 2 and
4, the array will look like this:
[1, 2, 4, 4].
If you are currently scratching your head, that is perfectly okay because when this one clicks, it clicks for good.
If you’re struggling, you should try taking out a pen and paper and step
through the solution provided above one step at a time. Keep track of
i, j, currElement,
arr[j], and the input arr itself
at every step. After going through this a few times, you’ll have
your “ah HA!” moment.
Insertion Sort runtime is O(n2) because:
In the worst case scenario where our input array is
entirely unsorted, since this algorithm contains a nested loop, its run
time behaves similarly to bubbleSort and
selectionSort. In this case, we are forced to make a
comparison at each iteration of the inner loop. Not convinced? Let’s
derive the complexity. We’ll use much of the same argument as we did in
selectionSort. Say we had the worst case scenario where are
input array is sorted in full decreasing order, but we wanted to sort it
in increasing order:
n is the length of the input arraycurrElement into
the sorted region. However, since we are discussing the case where the
data is already in decreasing order, the element must travel the maximum
distance to find it’s insertion point! We know this insertion point to
be index 0, since every currElement will be the next
smallest of the array. So:
The amount of memory consumed by the algorithm does not increase relative to the size of the input array. We use the same amount of memory and create the same amount of variables regardless of the size of our input. A quick indicator of this is the fact that we don’t create any arrays.
Insertion Sort has one advantage that makes it absolutely supreme in one special case. Insertion Sort is what’s known as an “online” algorithm. Online algorithms are great when you’re dealing with streaming data, because they can sort the data live as it is received.
If you must sort a set of data that is ever-incoming, for example, maybe you are sorting the most relevant posts in a social media feed so that those posts that are most likely to impact the site’s audience always appear at the top of the feed, an online algorithm like Insertion Sort is a great option.
Insertion Sort works well in this situation because the left side of the array is always sorted, and in the case of nearly sorted arrays, it can run in linear time. The absolute best case scenario for Insertion Sort is when there is only one unsorted element, and it is located all the way to the right of the array.
Well, if you have data constantly being pushed to the array, it will always be added to the right side. If you keep your algorithm constantly running, the left side will always be sorted. Now you have linear time sort.
Otherwise, Insertion Sort is, in general, useful in all the same situations as Bubble Sort. It’s a good option when:
You needed to come up with two pieces of code to make merge sort work.
Merging two sorted arrays is simple. Since both arrays are sorted, we know the smallest numbers to always be at the front of the arrays. We can construct the new array by comparing the first elements of both input arrays. We remove the smaller element from it’s respective array and add it to our new array. Do this until both input arrays are empty:
Remember the following about JavaScript to understand the above code.
0 is considered a falsey value, meaning it acts like
false when used in Boolean expressions. All other numbers
are truthy.
Infinity is a value that is guaranteed to be greater than
any other quantity
shift is an array method that removes and returns the first
element
Here’s the annotated version.
By using Infinity as the default element when an array is
empty, we are able to elegantly handle the scenario where one array
empties before the other. We know that any actual element will be less
than Infinity so we will continually take the other element
into our merged array.
In other words, we can safely handle this edge case:
Nice! We now have a way to merge two sorted arrays into a single sorted
array. It’s worth mentioning that merge will have a
O(n) runtime where n is the combined length of
the two input arrays. This is what we meant when we said it was “easy” to
merge two sorted arrays; linear time is fast! We’ll find fact this useful
later.
Now that we satisfied the merge idea, let’s handle the second point. That is, we say an array of 1 or 0 elements is already sorted. This will be the base case of our recursion. Let’s begin adding this code:
If our base case pertains to an array of a very small size, then the
design of our recursive case should make progress toward hitting this base
scenario. In other words, we should recursively call
mergeSort on smaller and smaller arrays. A logical way to do
this is to take the input array and split it into left and right halves.
Here is the part of the recursion where we do a lot of hand waving and we
take things on faith. We know that mergeSort will take in an
array and return the sorted version; we assume that it works. That means
the two recursive calls will return the sortedLeft and
sortedRight halves.
Okay, so we have two sorted arrays. We want to return one sorted array. So
merge them! Using the merge function we designed
earlier:
Wow. that’s it. Notice how light the implementation of
mergeSort is. Much of the heavy lifting (the actually
comparisons) is done by the merge helper.
mergeSort is a classic example of a “Divide and Conquer”
algorithm. In other words, we keep breaking the array into smaller and
smaller sub arrays. This is the same as saying we take the problem and
break it down into smaller and smaller subproblems. We do this until the
subproblems are so small that we trivially know the answer to them (an
array length 0 or 1 is already sorted). Once we have those subanswers we
can combine to reconstruct the larger problems that we previously divided
(merge the left and right subarrays).
n is the length of the input arrayO(log(n)).
3232 -> 16 -> 8 -> 4 -> 2 -> 1, we have to
split 5 times before reaching the base case,
log(32) = 5
merge function, which contributes O(n) in
isolation
merge in every recursive
mergeSort call, so the total complexity is
O(n * log(n))
Merge Sort is the first non-O(1) space sorting algorithm we’ve seen thus far.
The larger the size of our input array, the greater the number of subarrays we must create in memory. These are not free! They each take up finite space, and we will need a new subarray for each element in the original input. Therefore, Merge Sort has a linear space complexity, O(n).
Unless we, the engineers, have access in advance to some unique, exploitable insight about our dataset, it turns out that O(n log n) time is the best we can do when sorting unknown datasets.
That means that Merge Sort is fast! It’s way faster than Bubble Sort, Selection Sort, and Insertion Sort. However, due to its linear space complexity, we must always weigh the trade off between speed and memory consumption when making the choice to use Merge Sort. Consider the following:
Let’s begin structuring the recursion. The base case of any recursive problem is where the input is so trivial, we immediately know the answer without calculation. If our problem is to sort an array, what is the trivial array? An array of 1 or 0 elements! Let’s establish the code:
If our base case pertains to an array of a very small size, then the
design of our recursive case should make progress toward hitting this base
scenario. In other words, we should recursively call
quickSort on smaller and smaller arrays. This is very similar
to our previous mergeSort, except we don’t just split the
array down the middle. Instead we should arbitrarily choose an element of
the array as a pivot and partition the remaining elements relative to this
pivot:
Here is what to notice about the partition step above: 1. the pivot is an element of the array; we arbitrarily chose the first element 2. we removed the pivot from the master array before we filter into the left and right partitions
Now that we have the two subarrays of left and
right we have our subproblems! To solve these subproblems we
must sort the subarrays. I wish we had a function that sorts an array…oh
wait we do, quickSort! Recursively:
Okay, so we have the two sorted partitions. This means we have the two
subsolutions. But how do we put them together? Think about how we
partitioned them in the first place. Everything in
leftSorted is guaranteed to be less than
everything in rightSorted. On top of that,
pivot should be placed after the last element in
leftSorted, but before the first element in
rightSorted. So all we need to do is to combine the elements
in the order “left, pivot, right”!
That last concat line is a bit clunky. Bonus JS Lesson: we
can use the spread ... operator to elegantly concatenate
arrays. In general:
Utilizing that spread pattern gives us this final implementation:
That code was so clean we should show it again. Here’s the complete code
for your reference, for when you ctrl+F "quicksort" the night
before an interview:
Here is a summary of the complexity.
The runtime analysis of quickSort is more complex than
mergeSort
n is the length of the input arrayO(n)O(log(n)) recursive calls to reach the base case.
O(n) recursive calls to reach the base case.
Although we typically take the worst case when describing Big-O for an
algorithm, much research on quickSort has shown the worst
case to be an exceedingly rare occurrence even if we choose the pivot at
random. Because of this we still consider quickSort an
efficient algorithm. This is a common interview talking point, so you
should be familiar with the relationship between the choice of pivot and
efficiency of the algorithm.
Just in case: A somewhat common question a student may ask when studying
quickSort is, “If the median is the best pivot, why don’t we
always just choose the median when we partition?” Don’t overthink this. To
know the median of an array, it must be sorted in the first place.
Our implementation of quickSort uses O(n) space
because of the partition arrays we create. There is an in-place version of
quickSort that uses O(log(n)) space.
O(log(n)) space is not huge benefit over O(n).
You’ll also find our version of quickSort as easier to
remember, easier to implement. Just know that a O(logn) space
quickSort exists.
mergeSort.
If you know some constraints about dataset you can make some modifications
to optimize pivot choice. Here’s some food for thought. Our implementation
of quickSort will always take the first element as the pivot.
This means we will suffer from the worst case time complexity in the event
that we are given an already sorted array (ironic isn’t it?). If you know
your input data to be mostly already sorted, randomize the choice of pivot
- this is a very easy change. Bam. Solved like a true engineer.
We’ll implement binary search recursively. As always, we start with a base case that captures the scenario of the input array being so trivial, that we know the answer without further calculation. If we are given an empty array and a target, we can be certain that the target is not inside of the array:
Now for our recursive case. If we want to get a time complexity less than
O(n), we must avoid touching all n elements.
Adopting our dictionary strategy, let’s find the middle element and grab
references to the left and right halves of the sorted array:
It’s worth pointing out that the left and right halves do not contain the middle element we chose.
Here is where we leverage the sorted property of the array. If the target
is less than the middle, then the target must be in the left half of the
array. If the target is greater than the middle, then the target must be
in the right half of the array. So we can narrow our search to one of
these halves, and ignore the other. Luckily we have a function that can
search the half, its binarySearch:
We know binarySeach will return the correct Boolean, so we
just pass that result up by returning it ourselves. However, something is
lacking in our code. It is only possible to get a false from the literal
return false line, but there is no return true.
Looking at our conditionals, we handle the cases where the target is less
than middle or the target is greater than the middle, but what if the
product is equal to the middle? If the target is equal to
the middle, then we found the target and should return true!
This is easy to add with an else:
To wrap up, we have confidence of our base case will eventually be hit because we are continually halving the array. We halve the array until it’s length is 0 or we actually find the target.
Here is the code again for your quick reference:
The complexity analysis of this algorithm is easier to explain through visuals, so we highly encourage you to watch the lecture that accompanies this reading. In any case, here is a summary of the complexity:
n is the length of the input arraylog(n)
n = 8
8 -> 4 -> 2 -> 1
log(8) = 3
Our implementation uses n space due to half arrays we create
using slice. Note that JavaScript slice creates a new array,
so it requires additional memory to be allocated.
Use this algorithm when the input data is sorted!!! This is a heavy requirement, but if you have it, you’ll have an insanely fast algorithm. Of course, you can use one of your high-functioning sorting algorithms to sort the input and then perform the binary search!
This project contains a skeleton for you to implement Bubble Sort. In the file lib/bubble_sort.js, you should implement the Bubble Sort. This is a description of how the Bubble Sort works (and is also in the code file).
cd into the project foldernpm install to install dependencies in the project root
directory
npm test to run the specs/test/test.js. Your job is
to write code in the /lib/bubble_sort.js that implements
the Bubble Sort.
This project contains a skeleton for you to implement Selection Sort. In
the file lib/selection_sort.js, you should implement the
Selection Sort. You can use the same swap function from
Bubble Sort; however, try to implement it on your own, first.
The algorithm can be summarized as the following:
This is a description of how the Selection Sort works (and is also in the code file).
cd into the project foldernpm install to install dependencies in the project root
directory
npm test to run the specs/test/test.js. Your job is
to write code in the /lib/selection_sort.js that implements
the Selection Sort.
This project contains a skeleton for you to implement Insertion Sort. In the file lib/insertion_sort.js, you should implement the Insertion Sort.
The algorithm can be summarized as the following:
This is a description of how the Insertion Sort works (and is also in the code file).
cd into the project foldernpm install to install dependencies in the project root
directory
npm test to run the specs/test/test.js. Your job is
to write code in the /lib/insertion_sort.js that implements
the Insertion Sort.
This project contains a skeleton for you to implement Merge Sort. In the file lib/merge_sort.js, you should implement the Merge Sort.
The algorithm can be summarized as the following:
This is a description of how the Merge Sort works (and is also in the code file).
cd into the project foldernpm install to install dependencies in the project root
directory
npm test to run the specs/test/test.js. Your job is
to write code in the /lib/merge_sort.js that implements the
Merge Sort.
This project contains a skeleton for you to implement Quick Sort. In the file lib/quick_sort.js, you should implement the Quick Sort. This is a description of how the Quick Sort works (and is also in the code file).
cd into the project foldernpm install to install dependencies in the project root
directory
npm test to run the specs/test/test.js. Your job is
to write code in the /lib/quick_sort.js that implements the
Quick Sort.
This project contains a skeleton for you to implement Binary Search. In the file lib/binary_search.js, you should implement the Binary Search and its cousin Binary Search Index.
The Binary Search algorithm can be summarized as the following:
This is a description of how the Binary Search works (and is also in the code file).
Then you need to adapt that to return the index of the found item rather than a Boolean value. The pseudocode is also in the code file.
cd into the project foldernpm install to install dependencies in the project root
directory
npm test to run the specs/test/test.js. Your job is
to write code in the /lib/binary_search.js that implements
the Binary Search and Binary Search Index.
The objective of this lesson is for you to become comfortable with implementing common data structures. This is important because questions about data structures are incredibly likely to be interview questions for software engineers from junior to senior levels. Moreover, understanding how different data structures work will influence the libraries and frameworks that you choose when writing software.
When you are done, you will be able to:
When you are done, you will be able to:
In the university setting, it’s common for Linked Lists to appear early on in an undergraduate’s Computer Science coursework. While they don’t always have the most practical real-world applications in industry, Linked Lists make for an important and effective educational tool in helping develop a student’s mental model on what data structures actually are to begin with.
Linked lists are simple. They have many compelling, reoccurring edge cases to consider that emphasize to the student the need for care and intent while implementing data structures. They can be applied as the underlying data structure while implementing a variety of other prevalent abstract data types, such as Lists, Stacks, and Queues, and they have a level of versatility high enough to clearly illustrate the value of the Object Oriented Programming paradigm.
They also come up in software engineering interviews quite often.
A Linked List data structure represents a linear sequence of “vertices” (or “nodes”), and tracks three important properties.
Linked List Properties:
| Property | Description |
|---|---|
head |
The first node in the list. |
tail |
The last node in the list. |
length |
The number of nodes in the list; the list’s length. |
The data being tracked by a particular Linked List does not live inside the Linked List instance itself. Instead, each vertex is actually an instance of an even simpler, smaller data structure, often referred to as a “Node”.
Depending on the type of Linked List (there are many), Node instances track some very important properties as well.
Linked List Node Properties:
| Property | Description |
|---|---|
value |
The actual value this node represents. |
next |
The next node in the list (relative to this node). |
previous |
The previous node in the list (relative to this node). |
NOTE: The previous property is for Doubly
Linked Lists only!
Linked Lists contain ordered data, just like arrays. The first node in the list is, indeed, first. From the perspective of the very first node in the list, the next node is the second node. From the perspective of the second node in the list, the previous node is the first node, and the next node is the third node. And so it goes.
Admittedly, this does sound a lot like an Array so far, and that’s because Arrays and Linked Lists are both implementations of the List ADT. However, there is an incredibly important distinction to be made between Arrays and Linked Lists, and that is how they physically store their data. (As opposed to how they represent the order of their data.)
Recall that Arrays contain contiguous data. Each element of an array is actually stored next to it’s neighboring element in the actual hardware of your machine, in a single continuous block in memory.

An Array’s contiguous data being stored in a continuous block of addresses in memory.
Unlike Arrays, Linked Lists contain non-contiguous data. Though Linked Lists represent data that is ordered linearly, that mental model is just that - an interpretation of the representation of information, not reality.
In reality, in the actual hardware of your machine, whether it be in disk
or in memory, a Linked List’s Nodes are not stored in a single continuous
block of addresses. Rather, Linked List Nodes live at randomly distributed
addresses throughout your machine! The only reason we know which node
comes next in the list is because we’ve assigned its reference to the
current node’s next pointer.

A Singly Linked List’s non-contiguous data (Nodes) being stored at randomly distributed addresses in memory.
For this reason, Linked List Nodes have no indices, and no random access. Without random access, we do not have the ability to look up an individual Linked List Node in constant time. Instead, to find a particular Node, we have to start at the very first Node and iterate through the Linked List one node at a time, checking each Node’s next Node until we find the one we’re interested in.
So when implementing a Linked List, we actually must implement both the Linked List class and the Node class. Since the actual data lives in the Nodes, it’s simpler to implement the Node class first.
There are four flavors of Linked List you should be familiar with when walking into your job interviews.
Linked List Types:
| List Type | Description | Directionality |
|---|---|---|
| Singly Linked | Nodes have a single pointer connecting them in a single direction. | Head→Tail |
| Doubly Linked | Nodes have two pointers connecting them bi-directionally. | Head⇄Tail |
| Multiply Linked | Nodes have two or more pointers, providing a variety of potential node orderings. | Head⇄Tail, A→Z, Jan→Dec, etc. |
| Circularly Linked |
Final node’s next pointer points to the first node,
creating a non-linear, circular version of a Linked List.
|
Head→Tail→Head→Tail |
NOTE: These Linked List types are not always mutually exclusive.
For instance:
You are most likely to encounter Singly and Doubly Linked Lists in your upcoming job search, so we are going to focus exclusively on those two moving forward. However, in more senior level interviews, it is very valuable to have some familiarity with the other types of Linked Lists. Though you may not actually code them out, you will win extra points by illustrating your ability to weigh the tradeoffs of your technical decisions by discussing how your choice of Linked List type may affect the efficiency of the solutions you propose.
Linked Lists are great foundation builders when learning about data structures because they share a number of similar methods (and edge cases) with many other common data structures. You will find that many of the concepts discussed here will repeat themselves as we dive into some of the more complex non-linear data structures later on, like Trees and Graphs.
In the project that follows, we will implement the following Linked List methods:
| Type | Name | Description | Returns |
|---|---|---|---|
| Insertion | addToTail |
Adds a new node to the tail of the Linked List. | Updated Linked List |
| Insertion | addToHead |
Adds a new node to the head of the Linked List. | Updated Linked List |
| Insertion | insertAt |
Inserts a new node at the “index”, or position, specified. | Boolean |
| Deletion | removeTail |
Removes the node at the tail of the Linked List. | Removed node |
| Deletion | removeHead |
Removes the node at the head of the Linked List. | Removed node |
| Deletion | removeFrom |
Removes the node at the “index”, or position, specified. | Removed node |
| Search | contains |
Searches the Linked List for a node with the value specified. | Boolean |
| Access | get |
Gets the node at the “index”, or position, specified. | Node at index |
| Access | set |
Updates the value of a node at the “index”, or position, specified. | Boolean |
| Meta | size |
Returns the current size of the Linked List. | Integer |
Before we begin our analysis, here is a quick summary of the Time and Space constraints of each Linked List Operation. The complexities below apply to both Singly and Doubly Linked Lists:
| Data Structure Operation | Time Complexity (Avg) | Time Complexity (Worst) | Space Complexity (Worst) |
|---|---|---|---|
| Access | Θ(n) |
O(n) |
O(n) |
| Search | Θ(n) |
O(n) |
O(n) |
| Insertion | Θ(1) |
O(1) |
O(n) |
| Deletion | Θ(1) |
O(1) |
O(n) |
Before moving forward, see if you can reason to yourself why each operation has the time and space complexity listed above!
Unlike Arrays, Linked Lists Nodes are not stored contiguously in memory, and thereby do not have an indexed set of memory addresses at which we can quickly lookup individual nodes in constant time. Instead, we must begin at the head of the list (or possibly at the tail, if we have a Doubly Linked List), and iterate through the list until we arrive at the node of interest.
In Scenario 1, we’ll know we’re there because we’ve iterated 8 times. In Scenario 2, we’ll know we’re there because, while iterating, we’ve checked each node’s value and found one that matches our target value, “Q”.
In the worst case scenario, we may have to traverse the entire Linked List until we arrive at the final node. This makes both Access & Search Linear Time operations.
Since we have our Linked List Nodes stored in a non-contiguous manner that
relies on pointers to keep track of where the next and previous nodes
live, Linked Lists liberate us from the linear time nature of Array
insertions and deletions. We no longer have to adjust the position at
which each node/element is stored after making an insertion at a
particular position in the list. Instead, if we want to insert a new node
at position i, we can simply:
next and previous pointers
to the nodes that live at positions i and
i - 1, respectively.
next pointer of the node that lives at position
i - 1 to point to the new node.
previous pointer of the node that lives at
position i to point to the new node.
And we’re done, in Constant Time. No iterating across the entire list necessary.
“But hold on one second,” you may be thinking. “In order to insert a new node in the middle of the list, don’t we have to lookup its position? Doesn’t that take linear time?!”
Yes, it is tempting to call insertion or deletion in the middle of a Linked List a linear time operation since there is lookup involved. However, it’s usually the case that you’ll already have a reference to the node where your desired insertion or deletion will occur.
For this reason, we separate the Access time complexity from the Insertion/Deletion time complexity, and formally state that Insertion and Deletion in a Linked List are Constant Time across the board.
Without a reference to the node at which an insertion or deletion will occur, due to linear time lookup, an insertion or deletion in the middle of a Linked List will still take Linear Time, sum total.
It’s obvious that Linked Lists have one node for every one item in the list, and for that reason we know that Linked Lists take up Linear Space in memory. However, when asked in an interview setting what the Space Complexity of your solution to a problem is, it’s important to recognize the difference between the two scenarios above.
In Scenario 1, we are not creating a new Linked List. We simply need to operate on the one given. Since we are not storing a new node for every node represented in the Linked List we are provided, our solution is not necessarily linear in space.
In Scenario 2, we are creating a new Linked List. If the number of nodes we create is linearly correlated to the size of our input data, we are now operating in Linear Space.
Linked Lists can be traversed both iteratively and recursively. If you choose to traverse a Linked List recursively, there will be a recursive function call added to the call stack for every node in the Linked List. Even if you’re provided the Linked List, as in Scenario 1, you will still use Linear Space in the call stack, and that counts.
Stacks and Queues aren’t really “data structures” by the strict definition of the term. The more appropriate terminology would be to call them abstract data types (ADTs), meaning that their definitions are more conceptual and related to the rules governing their user-facing behaviors rather than their core implementations.
For the sake of simplicity, we’ll refer to them as data structures and ADTs interchangeably throughout the course, but the distinction is an important one to be familiar with as you level up as an engineer.
Now that that’s out of the way, Stacks and Queues represent a linear collection of nodes or values. In this way, they are quite similar to the Linked List data structure we discussed in the previous section. In fact, you can even use a modified version of a Linked List to implement each of them. (Hint, hint.)
These two ADTs are similar to each other as well, but each obey their own special rule regarding the order with which Nodes can be added and removed from the structure.
Since we’ve covered Linked Lists in great length, these two data structures will be quick and easy. Let’s break them down individually in the next couple of sections.
Stacks are a Last In First Out (LIFO) data structure. The last Node added to a stack is always the first Node to be removed, and as a result, the first Node added is always the last Node removed.
The name Stack actually comes from this characteristic, as it is helpful to visualize the data structure as a vertical stack of items. Personally, I like to think of a Stack as a stack of plates, or a stack of sheets of paper. This seems to make them more approachable, because the analogy relates to something in our everyday lives.
If you can imagine adding items to, or removing items from, a Stack of…literally anything…you’ll realize that every (sane) person naturally obeys the LIFO rule.
We add things to the top of a stack. We remove things from the top of a stack. We never add things to, or remove things from, the bottom of the stack. That’s just crazy.
Note: We can use JavaScript Arrays to implement a basic stack.
Array#push adds to the top of the stack and
Array#pop will remove from the top of the stack. In the
exercise that follows, we’ll build our own Stack class from scratch
(without using any arrays). In an interview setting, your evaluator may be
okay with you using an array as a stack.
Queues are a First In First Out (FIFO) data structure. The first Node added to the queue is always the first Node to be removed.
The name Queue comes from this characteristic, as it is helpful to visualize this data structure as a horizontal line of items with a beginning and an end. Personally, I like to think of a Queue as the line one waits on for an amusement park, at a grocery store checkout, or to see the teller at a bank.
If you can imagine a queue of humans waiting…again, for literally anything…you’ll realize that most people (the civil ones) naturally obey the FIFO rule.
People add themselves to the back of a queue, wait their turn in line, and make their way toward the front. People exit from the front of a queue, but only when they have made their way to being first in line.
We never add ourselves to the front of a queue (unless there is no one else in line), otherwise we would be “cutting” the line, and other humans don’t seem to appreciate that.
Note: We can use JavaScript Arrays to implement a basic queue.
Array#push adds to the back (enqueue) and
Array#shift will remove from the front (dequeue). In the
exercise that follows, we’ll build our own Queue class from scratch
(without using any arrays). In an interview setting, your evaluator may be
okay with you using an array as a queue.
Translator: CarrieOn
Author: labuladong
It’s easy to reverse a single linked list using iteration, however it’s kind of difficult to come up with a recursive solution. Furthermore, if only part of a linked list needs reversed, can you nail it with recursion?
If you haven’t known how to recursively reverse a single linked list, no worry, we will start right here and guide you step by step to a deeper level.
To reverse part of a linked list means we only reverse elements in a specific interval and leave others untouched.

Note: Index starts from 1. Two loops needed if solve via iteration: use one for-loop to find the mth element, and then use another for-loop to reverse elements between m and n. While in recursive solution, no loop at all.
Though iterative solution looks simple, you have to be careful with the details. On the contrary, recursive solution is quite elegant. Let’s start reversing a whole single linked list in the recursive way.
You may have already known the solution below.
Do you feel lost in trying to understand code above? Well, you are not the only one. This algorithm is often used to show how clever and elegant recursion can be. Let’s dig into the code together.
For recursion,
the most important thing is to clarify the definition of the recursive
function. Specifically, we define reverse as follows:
Input a node head , we will reverse the list starting from
head , and return the new head node.
After clarifying the definition, we look back at the problem. For example, we want to reverse the list below:

So after calling reverse(head) , recursion happens:
Did you just step into the messy details in recursion? Oops, it’s a wrong way, step back now! Focus on the recursion definition (which tells you what it does) to understand how recursive code works the wonder.

After executing reverse(head.next) , the whole linked list
becomes this:

According to the definition of the recursive function,
reverse needs to return the new head node, so we use variable
last to mark it.
Let’s continue cracking the next piece of code:

Last work to do:

The whole linked list is successfully reversed now. Amazing, isn’t it?
Last but not the least, there are two things in recursion you need to pay attention to:
java if(head.next == null) return head;
last, and the former
head becomes the last node, don’t forget to point its tail
to null.
java head.next = null;
After understanding above, now we can proceed further, the problem below is actually an extend to the above solution.
This time we will implement a funtion below:
Take below as an example, call reverseN(head, 3) :

The idea is similar to reversing the whole linked list, only a few modifications needed:
Main differences:
n == 1, if reverse only one element, then new
head is itself, meanwhile
remember to mark the successor node.
head.next directly to null,
because after reversing the whole list, head becoms the last node. But
now head may not be the last node after reversion, so we
need mark successor (the (n+1)th node), and link it to
head after reversion.

OK, now we are pretty close to reversing part of the linked list.
Given an interval [m,n] (index starts from 1), only reverse
elements in this section.
First, if m == 1 , it is equal to reversing the first
n elements as we discussed just now.
What if m != 1 ? If we take the index of the
head as 1, then we need to reverse from the
mth element. And what if we take the index of the
head.next as 1? Then compared to head.next , the
reverse section should start from (m-1)th element. And what
about head.next.next …
Different from iteration, this is how we think in the recursive way, so our code should be:
Stacks and Queues are so similar in composition that we can discuss their properties together. They track the following three properties:
Stack Properties | Queue Properties:
| Stack Property | Description | Queue Property | Description |
|---|---|---|---|
top |
The first node in the Stack | front |
The first node in the Queue. |
| —- | Stacks do not have an equivalent | back |
The last node in the Queue. |
length |
The number of nodes in the Stack; the Stack’s length. | length |
The number of nodes in the Queue; the Queue’s length. |
Notice that rather than having a head and a
tail like Linked Lists, Stacks have a top, and
Queues have a front and a back instead. Stacks
don’t have the equivalent of a tail because you only ever
push or pop things off the top of Stacks. These properties are essentially
the same; pointers to the end points of the respective List ADT where
important actions way take place. The differences in naming conventions
are strictly for human comprehension.
Similarly to Linked Lists, the values stored inside a Stack or a Queue are actually contained within Stack Node and Queue Node instances. Stack, Queue, and Singly Linked List Nodes are all identical, but just as a reminder and for the sake of completion, these List Nodes track the following two properties:
Stack & Queue Node Properties:
| Property | Description |
|---|---|
value |
The actual value this node represents. |
next |
The next node in the Stack (relative to this node). |
In the exercise that follows, we will implement a Stack data structure along with the following Stack methods:
| Type | Name | Description | Returns |
|---|---|---|---|
| Insertion | push |
Adds a Node to the top of the Stack. | Integer - New size of stack |
| Deletion | pop |
Removes a Node from the top of the Stack. | Node removed from top of Stack |
| Meta | size |
Returns the current size of the Stack. | Integer |
In the exercise that follows, we will implement a Queue data structure along with the following Queue methods:
| Type | Name | Description | Returns |
|---|---|---|---|
| Insertion | enqueue |
Adds a Node to the front of the Queue. | Integer - New size of Queue |
| Deletion | dequeue |
Removes a Node from the front of the Queue. | Node removed from front of Queue |
| Meta | size |
Returns the current size of the Queue. | Integer |
Before we begin our analysis, here is a quick summary of the Time and Space constraints of each Stack Operation.
| Data Structure Operation | Time Complexity (Avg) | Time Complexity (Worst) | Space Complexity (Worst) |
|---|---|---|---|
| Access | Θ(n) |
O(n) |
O(n) |
| Search | Θ(n) |
O(n) |
O(n) |
| Insertion | Θ(1) |
O(1) |
O(n) |
| Deletion | Θ(1) |
O(1) |
O(n) |
Before moving forward, see if you can reason to yourself why each operation has the time and space complexity listed above!
When the Stack ADT was first conceived, its inventor definitely did not prioritize searching and accessing individual Nodes or values in the list. The same idea applies for the Queue ADT. There are certainly better data structures for speedy search and lookup, and if these operations are a priority for your use case, it would be best to choose something else!
Search and Access are both linear time operations for Stacks and Queues,
and that shouldn’t be too unclear. Both ADTs are nearly identical to
Linked Lists in this way. The only way to find a Node somewhere in the
middle of a Stack or a Queue, is to start at the top (or the
back) and traverse downward (or forward) toward the
bottom (or front) one node at a time via each
Node’s next property.
This is a linear time operation, O(n).
For Stacks and Queues, insertion and deletion is what it’s all about. If
there is one feature a Stack absolutely must have, it’s constant time
insertion and removal to and from the top of the Stack
(FIFO). The same applies for Queues, but with insertion occurring at the
back and removal occurring at the front (LIFO).
Think about it. When you add a plate to the top of a stack of plates, do you have to iterate through all of the other plates first to do so? Of course not. You simply add your plate to the top of the stack, and that’s that. The concept is the same for removal.
Therefore, Stacks and Queues have constant time Insertion and Deletion via
their push and pop or enqueue and
dequeue methods, O(1).
The space complexity of Stacks and Queues is very simple. Whether we are instantiating a new instance of a Stack or Queue to store a set of data, or we are using a Stack or Queue as part of a strategy to solve some problem, Stacks and Queues always store one Node for each value they receive as input.
For this reason, we always consider Stacks and Queues to have a linear space complexity, O(n).
At this point, we’ve done a lot of work understanding the ins and outs of Stacks and Queues, but we still haven’t really discussed what we can use them for. The answer is actually…a lot!
For one, Stacks and Queues can be used as intermediate data structures while implementing some of the more complicated data structures and methods we’ll see in some of our upcoming sections.
For example, the implementation of the breadth-first Tree traversal algorithm takes advantage of a Queue instance, and the depth-first Graph traversal algorithm exploits the benefits of a Stack instance.
Additionally, Stacks and Queues serve as the essential underlying data structures to a wide variety of applications you use all the time. Just to name a few:
pushing that event to
a Stack.
poped off the Stack, because the last event that
occured should be the first one to be undone (LIFO).
pushed back onto the Stack.
The objective of this lesson is for you to become comfortable with implementing common data structures. This is important because questions about data structures are incredibly likely to be interview questions for software engineers from junior to senior levels. Moreover, understanding how different data structures work will influence the libraries and frameworks that you choose when writing software.
When you are done, you will be able to:
When you are done, you will be able to:
Let’s explore the Heap data structure! In particular, we’ll explore Binary Heaps. A binary heap is a type of binary tree. However, a heap is not a binary search tree. A heap is a partially ordered data structure, whereas a BST has full order. In a heap, the root of the tree will be the maximum (max heap) or the minimum (min heap). Below is an example of a max heap:

max_heap
Notice that the heap above does not follow search tree property where all values to the left of a node are less and all values to the right are greater or equal. Instead, the max heap invariant is:
This constraint makes heaps much more relaxed in structure compared to a search tree. There is no guaranteed order among “siblings” or “cousins” in a heap. The relationship only flows down the tree from parent to child. In other words, in a max heap, a node will be greater than all of it’s children, it’s grandchildren, its great-grandchildren, and so on. A consequence of this is the root being the absolute maximum of the entire tree. We’ll be exploring max heaps together, but these arguments are symmetric for a min heap.
We’ll eventually implement a max heap together, but first we’ll need to take a quick detour. Our design goal is to implement a data structure with efficient operations. Since a heap is a type of binary tree, recall the circumstances where we had a “best case” binary tree. We’ll need to ensure our heap has minimal height, that is, it must be a balanced tree!
Our heap implementation will not only be balanced, but it will also be complete. To clarify, every complete tree is also a balanced tree, but not every balanced tree is also complete. Our definition of a complete tree is:
Here are few examples of the definition:

complete_tree
Notice that the tree is on the right fails the second point of our definition because there is a gap in the last level. Informally, you can think about a complete tree as packing its nodes as closely together as possible. This line of thinking will come into play when we code heaps later.
Heaps are the most useful when attacking problems that require you to “partially sort” data. This usually takes form in problems that have us calculate the largest or smallest n numbers of a collection. For example: What if you were asked to find the largest 5 numbers in an array in linear time, O(n)? The fastest sorting algorithms are O(n logn), so none of those algorithms will be good enough. However, we can use a heap to solve this problem in linear time.
We’ll analyze this in depth when we implement a heap in the next section!
One of the most common uses of a binary heap is to implement a “priority queue”. We learned before that a queue is a FIFO (First In, First Out) data structure. With a priority queue, items are removed from the queue based on a priority number. The priority number is used to place the items into the heap and pull them out in the correct priority order!
Now that we are familiar with the structure of a heap, let’s implement one! What may be surprising is that the usual way to implement a heap is by simply using an array. That is, we won’t need to create a node class with pointers. Instead, each index of the array will represent a node, with the root being at index 1. We’ll avoid using index 0 of the array so our math works out nicely. From this point, we’ll use the following rules to interpret the array as a heap:
i represents a node in the heapi can be found at index
2 * i
i can be found at index
2 * i + 1
In other words, the array
[null, 42, 32, 24, 30, 9, 20, 18, 2, 7] represents the heap
below. Take a moment to analyze how the array indices work out to
represent left and right children.

max_heap
Pretty clever math right? We can also describe the relationship from child
to parent node. Say we are given a node at index i in the
heap, then it’s parent is found at index Math.floor(i / 2).
It’s useful to visualize heap algorithms using the classic image of nodes and edges, but we’ll translate that into array index operations.
What’s a heap if we can’t add data into it? We’ll need a
insert method that will add a new value into the heap without
voiding our heap property. In our MaxHeap, the property
states that a node must be greater than its children.
siftUp
push the new value to the end of the arrayThis is the “fetch” operation of a heap. Since we maintain heap property throughout, the root of the heap will always be the maximum value. We want to delete and return the root, whilst keeping the heap property.
siftDown.
O(log(n))O(log(n))
Recall that our heap will be a complete/balanced tree. This means it’s
height is log(n) where n is the number of items.
Both insert and deleteMax have a time complexity
of log(n) because of siftUp and
siftDown respectively. In worst case insert, we
will have to siftUp a leaf all the way to the root of the
tree. In the worst case deleteMax, we will have to
siftDown the new root all the way down to the leaf level. In
either case, we’ll have to traverse the full height of the tree,
log(n).
Now that we have established O(log(n)) for a single
insertion, let’s analyze the time complexity for turning an array into a
heap (we call this heapify, coming in the next project :)). The algorithm
itself is simple, just perform an insert for every element.
Since there are n elements and each insert requires
log(n) time, our total complexity for heapify is
O(nlog(n))… Or is it? There is actually a tighter bound on
heapify. The proof requires some math that you won’t find valuable in your
job search, but do understand that the true time complexity of heapify is
amortized O(n). Amortized refers to the fact that our
analysis is about performance over many insertions.
O(n), since we use a single array to store heap data.heap,
let’s implement one! What may be surprising is that the usual way to
implement a heap is by simply using an array. That is, we won’t need to
create a node class with pointers. Instead, each index of the array will
represent a node, with the root being at index 1. We’ll avoid using
index 0 of the array so our math works out nicely. From this point,
we’ll use the following rules to interpret the array as a heap:
i represents a node in the heapi can be found at index
2 * i
i can be found at index
2 * i + 1
In other words, the array
[null, 42, 32, 24, 30, 9, 20, 18, 2, 7] represents the heap
below. Take a moment to analyze how the array indices work out to
represent left and right children.

max_heap
Pretty clever math right? We can also describe the relationship from child
to parent node. Say we are given a node at index i in the
heap, then it’s parent is found at index Math.floor(i / 2).
It’s useful to visualize heap algorithms using the classic image of nodes and edges, but we’ll translate that into array index operations.
What’s a heap if we can’t add data into it? We’ll need a
insert method that will add a new value into the heap without
voiding our heap property. In our MaxHeap, the property
states that a node must be greater than its children.
siftUp
push the new value to the end of the arrayThis is the “fetch” operation of a heap. Since we maintain heap property throughout, the root of the heap will always be the maximum value. We want to delete and return the root, whilst keeping the heap property.
siftDown.
O(log(n))O(log(n))
Recall that our heap will be a complete/balanced tree. This means it’s
height is log(n) where n is the number of items.
Both insert and deleteMax have a time complexity
of log(n) because of siftUp and
siftDown respectively. In worst case insert, we
will have to siftUp a leaf all the way to the root of the
tree. In the worst case deleteMax, we will have to
siftDown the new root all the way down to the leaf level. In
either case, we’ll have to traverse the full height of the tree,
log(n).
Now that we have established O(log(n)) for a single
insertion, let’s analyze the time complexity for turning an array into a
heap (we call this heapify, coming in the next project :)). The algorithm
itself is simple, just perform an insert for every element.
Since there are n elements and each insert requires
log(n) time, our total complexity for heapify is
O(nlog(n))… Or is it? There is actually a tighter bound on
heapify. The proof requires some math that you won’t find valuable in your
job search, but do understand that the true time complexity of heapify is
amortized O(n). Amortized refers to the fact that our
analysis is about performance over many insertions.
O(n), since we use a single array to store heap data.
We’ve emphasized heavily that heaps are a partially ordered data
structure. However, we can still leverage heaps in a sorting algorithm to
end up with fully sorted array. The strategy is simple using our previous
MaxHeap implementation:
insert all elements of the array into a
MaxHeap
deleteMax until the
heap is empty, every deletion will return the next element in decreasing
order
The code is straightforward:
n is the size of the input arrayO(n) time as previously discussedn steps in isolation and each
deleteMax will require log(n) steps to restore
max heap property (due to sifting-down). This means step 2 costs
O(nlog(n))
O(n + nlog(n)) = O(nlog(n))
So heapSort performs as fast as our other efficient sorting
algorithms, but how does it fair in space complexity? Our implementation
above requires an extra O(n) amount of space because the heap
is maintained separately from the input array. If we can figure out a way
to do all of these heap operations in-place we can get constant
O(1) space! Let’s work on this now.
The in-place algorithm will have the same 2 steps, but it will differ in the implementation details. Since we need to have all operations take place in a single array, we’re going to have to denote two regions of the array. That is, we’ll need a heap region and a sorted region. We begin by turning the entire region into a heap. Then we continually delete max to get the next element in increasing order. As the heap region shrinks, the sorted region will grow.
Let’s focus on designing step-1 as an in-place algorithm. In other words,
we’ll need to reorder elements of the input array so they follow max heap
property. This is usually refered to as heapify. Our
heapify will use much of the same logic as
MaxHeap#siftDown.
We weren’t kidding when we said this would be similar to
MaxHeap#siftDown. If you are not convinced, flip to the
previous section and take a look! The few differences we want to emphasize
are:
i, it’s left index is
2 * i + 1 and it’s right index is 2 * i + 2
n represents the number of nodes in the heap
array.length also represents the
number of nodes in the heap. That is true, but only in step-1. Later
we will need to dynamically state the size of the heap. Remember, we
are trying to do this without creating any extra arrays. We’ll need
to separate the heap and sorted regions of the array and
n will dictate the end of the heap.
swap helper function.
To correctly convert the input array into a heap, we’ll need to call
heapify on children nodes before their parents. This is easy
to do, just call heapify on each element right-to-left in the
array:
Nice! Now the elements of the array have been moved around to obey max heap property.
To put everything together, we’ll need to continually “delete max” from our heap. From our previous lecture, we learned the steps for deletion are to swap the last node of the heap into the root and then sift the new root down to restore max heap property. We’ll follow the same logic here, except we’ll need to account for the sorted region of the array. The array will contain the heap region in the front and the sorted region at the rear:
You’ll definitely want to watch the lecture that follows this reading to get a visual of how the array is divided into the heap and sorted regions.